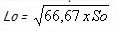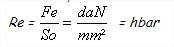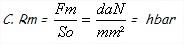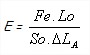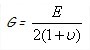Sommaire pour la partie suivante du Chapitre 1 de l’ouvrage de Jean Maton “Technologie du soudage”
Cette partie traite des essais mécaniques et dans un premier temps de l’essai de traction. Si vous souhaitez voir la partie qui traite des propriétés physiques et mécaniques des matériaux ou l’essai de dureté
1.3 ESSAIS MECANIQUES- 1.3.1 Essai de traction
- 1.3.2 Essais de dureté ( Hardness test )
- 1.3.3 Essai de résilience Charpy ( Ingénieur français 1864 – 1945 )
- 1.3.4 Essai de dureté “Shore”
- 1.3.5 Essais de pliage
1.3.1) Essai de traction
Cet essai est réglementé par la norme EN 10002-1. Il consiste à exercer, sur une éprouvette normalisée cylindrique Ø ≥ 4mm ou parallélépipédique e ≥ 3mm lisse et bien calibrée dans le matériau à tester Fig 1-1, deux actions mécaniques opposées qui vont la déformer progressivement, puis la rompre. Notons que la norme EN 10002-1 est remplacée par la norme ISO 6892-1 ( 2009 ), mais néanmoins reste toujours utilisée dans les milieux industriels.
- So = section initiale (mm²),
- Lo = longueur initiale entre a et b (mm),
- Lc = longueur de la partie calibrée (en mm),
- Su = section minimale après rupture ( mm²)
- Lu = longueur ultime après ruptures (mm)
Remarque : 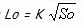
La vitesse de l’essai doit être faible et dépendra du matériau à tester.
Exemples : vmax ≤ 0,15 x Lo ( mm/min ) pour l’acier
vmax ≤ 0,009 x Lo ” pour l’aluminium
vmax ≤ 0,006 x Lo ” pour le cuivre
La Fig 1-2 montre un exemple de machine de traction actuelle. Les extrémités sont pincées dans les mâchoires de la machine de traction, comportant un dispositif enregistreur.

La traction ( ou charge ) s’exerce lentement suivant l’axe géométrique de l’éprouvette, qui va s’allonger. A un instant donné, une région de la partie médiane se ternit, l’éprouvette s’étrangle et le métal semble
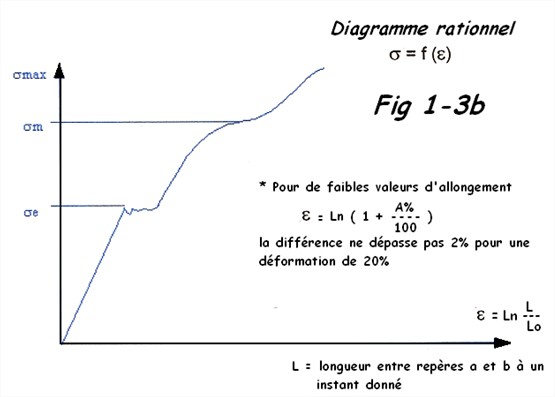
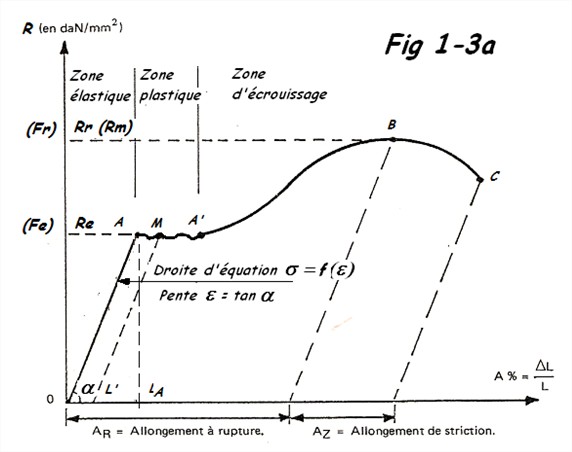
s’écouler à la façon d’un liquide très visqueux. C’est le phénomène de striction qui est rapidement suivi de la rupture. L’ordinateur ou un stylet enregistre un graphique qui mesure l’allongement de l’éprouvette en fonction de l’effort de traction ( F ) appliqué, ou encore de la contrainte ( σ ). On obtient un diagramme conventionnel ( effort – déformation ) donné en exemple à la Fig 1-3a ou un diagramme rationnel
( σ = f(ε ) ) tel que représenté à la Fig 1-3b.
Le diagramme se décompose en quatre phases ( Fig 1-3a ):
- Phase OA : Zone rectiligne, pour laquelle les allongements sont proportionnels aux efforts appliqués. C’est la zone élastique qui est réversible. Car, si l’on supprime l’effort de traction, le retour à l’équilibre se fait suivant la droite MM’, parallèle à OA et l’éprouvette conserve un allongement rémanent OM’.
- Phase A’B : La charge croît à nouveau avec les allongements jusqu’au point B. Il y a apparition de l’étranglement.
- Phase BC : L’allongement continue bien que la charge soit décroissante, jusqu’au point C, qui correspond à la rupture. Dans cette dernière phase, la déformation plastique est localisée dans une faible portion de l’éprouvette et n’est plus homogène. Il y a striction.
L’essai permet de mesurer :
– La limite élastique (Re ) qui représente la contrainte à partir de laquelle les allongements deviennent permanents et qui correspond sensiblement au seuil à partir duquel il n’y a plus de proportionnalité entre contrainte et allongement ( point A ). Par convention, la limite élastique est définie comme étant la contrainte correspondant à un allongement rémanent de 0,2 % ( Re0,2 ou Rp0,2 ).
Fe = effort de traction en A
So = section initiale = 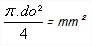
– La contrainte de rupture à la traction ( Rr ou Rm ) qui correspond au point B, bien que la rupture proprement dite a lieu en
– Le module d’élasticité longitudinale ( E ) appelé également ” Module de Young “, 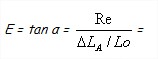
Le module d’élasticité longitudinale est le rapport de proportionnalité dans la zone élastique, qui existe entre les charges unitaires ( contraintes ) R( ) ou σ( ) et les allongements relatifs ΔL/L. Il caractérise l’aptitude d’un matériau à se déformer dans la période élastique.
Quelques valeurs usuelles de E ( exprimées en MPa = N/mm² ).
Aciers : 200000 à 220000
Tungstène : 420000
Acier inox : 198000
Fontes à graphite sphéroïdal : 16000 à 190000
Cuivre : 126000
Plomb : 17000
Fontes à graphite lamellaire : 120000
Alliages d’aluminium : 70000 à 75000
ν = coefficient de Poisson exprimant le rapport entre la déformation longitudinale et la déformation transversale de l’éprouvette de l’éprouvette soit 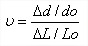
– Allongement à rupture Δr et allongement de striction Δz : La mesure se fait généralement sur la longueur entre les repères. On mesure alors Lu ( après rupture ). A% = 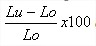
– Le palier AA’ : C’est le palier de ductilité, c’est-à-dire la réserve de sécurité ( plasticité ).
Ce palier est de plus court en fonction que la teneur en carbone des aciers augmente
( plus Re augmente). C’est pourquoi, seuls les aciers doux ( faible taux de carbone ) sont autorisés en construction métallique ( C = 0,2 % en moyenne )..
Exercice numérique
Soit une éprouvette cylindrique en acier de section initiale So = 150 mm². On lui applique une charge Fe = 3525 daN augmentant jusque Fm = 5400 daN. Après rupture Lu = 87,2 mm et ΔLA au point A = 0,08 mm. On demande de déterminer la valeur de Re, Rm (Rr ), Lo A% et G.


Si vous souhaitez voir la partie qui traite des propriétés physiques et mécaniques des matériaux ou l’essai de dureté
Ou si vous souhaitez retourner à la table des matières