


3.5 CONTRAINTES ADMISSIBLES DANS UNE TUYAUTERIE
3.5.1 CRITERES DE BASE POUR L'ETABLISSEMENT DES CONTRAINTES ADMISSIBLES( ANSI B31 )
En tout point de la tuyauterie:
- Contraintes primaires : Ce sont les contraintes résultant de l'action de la pression, du poids de la tuyauterie, ainsi que toute autre charge permanente ou occasionnelle ( vent, coup de bélier, séismes, ... ) qui doivent être limitées pour éviter tout risque d'instabilité plastique et de rupture. En principe, ces contraintes ne peuvent excéder la limite élastique du matériau, ni sa limite de résistance au fluage.
- Exemple d'instabilité plastique entre 2 supports: Les contraintes dues au poids et à la pression sont maximales au centre du tronçon et au droit des appuis. Si ces contraintes totales dépassent la limite élastique, la tuyauterie va se déformer jusqu'à la ruine complète, sans aucune stabilisation possible.
- Contraintes secondaires ( fatigue ) : Dues à l'amplitude, ou la variation, entre l'état chaud et l'état froid, des contraintes résultant de l'expansion thermique entravées de la tuyauterie ainsi que des déplacements des ancrages ( Ds sur les graphiques FIG 3-104 ) additionnées des contraintes primaires doivent être limitées pour éviter les 2 risques ci-après:
- Accroissement des déformations plastiques à chaque cycle de montée en température et de refroidissement, ce qui empêche une adaptation élastique et conduit assez rapidement à la rupture.
- Rupture par fatigue. C'est là la principale cause de rupture d'une tuyauterie et c'est elle qui détermine essentiellement les valeurs de contraintes admissibles fixées par les codes.
Remarque: sp + ss £ 3 Sm Sm £
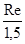
3.5.2 DONNEES DE BASE POUR LE CALCUL DES CONTRAINTES
Le calcul des contraintes doit être tiré d'un calcul de flexibilité ( ou de souplesse ) effectué avec la valeur à froid du module de YOUNG du matériau de la tuyauterie, c'est-à -dire, en considérant qu'il se produira toujours une relaxation totale des contraintes à chaud. En outre, ces calculs doivent être basés sur les dimensions minimales des tuyauteries, c'est-à -dire l'épaisseur commandée pour les tubes et autres composants, diminuée de la surépaisseur de corrosion et de la tolérance de laminage.
3.5.3 CONTRAINTES ADMISSIBLES INDUITES DANS UNE TUYAUTERIE SUIVANT LES CODES ANSI B31-1 ET 3
En conformité avec le § 3.5.2, les codes ANSI imposent les évaluations et les limitations des contraintes suivantes:
1. Contraintes dues aux charges mécaniques permanentes ( ANSI B31-1 )
Dans toute section de la tuyauterie, l'équation suivante devra être vérifiée:
SL =
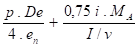
SL = contrainte longitudinale ( N/mm² )
P = pression de calcul ( N/mm² )
e = diamètre extérieur de la tuyauterie ( mm )
en = épaisseur nominale de la tuyauterie ( mm ) hors surépaisseur de corrosion et tolérance de laminage
I/v = module de flexion de la tuyauterie ( mm³ )
i = coefficient d'intensification des contraintes donné à la FIG 3-100 ( le produit 0,75 i ne peut jamais être inférieur à 1)
MA = moment résultant dans la section considérée dû aux charges mécaniques permanentes ( poids, pression, .... ) ( mmN )
Sh = contrainte admissible à la température de calcul pour le matériau ( N/mm² ) ( FIG 1-30 )
Remarque: le terme
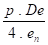
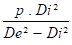
2. Contraintes dues à la combinaison des charges mécaniques permanentes et des charges mécaniques occasionnelles ( ANSI B31.1 )
L'équation ci-dessous doit être vérifiée en toute section de la tuyauterie.
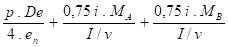
Dans le cas de séisme, on ne considère que la demi-amplitude de MB dû à ce séisme.
K' = 1,115 dans le cas de charges mécaniques occasionnelles se produisant pendant moins de 10% du temps de fonctionnement de la tuyauterie.
K' = 1,2 idem, mais ces charges ne se produisent que pendant moins de 1% de ce temps de fonctionnement.
Remarque: Le terme
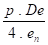
Pour l' ANSI B31.3, la somme des contraintes longitudinales SL et de celles dues aux charges occasionnelles ne peut excéder 1,33 Sh.
3. Contraintes causées par l'expansion thermique ( ANSI B31.1 )
L'équation ci-dessous doit être vérifiée en toute section de la tuyauterie.
SE =
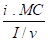
Avec : MC = amplitude du moment résultant dans la section considérée, dû à l'expansion thermique entravée de la tuyauterie ( mmN )
SA = f(1,25 Sc + 0,25 Sh ) = amplitude admissible des contraintes d'expansion thermique ( l'origine de cette valeur sera étudiée au paragraphe suivant ).
Sc = contrainte admissible à la température ambiante pour le matériau de la tuyauterie ( N/mm² )
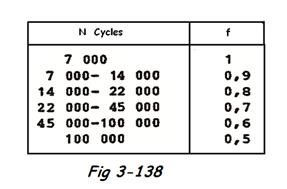
f = facteur de réduction de l'amplitude de contrainte admissible en fonction du nombre de cycles complets ( N ) de température susceptible de se produire pendant la durée de vie de la tuyauterie.
N = 7000 est la valeur prise comme base par l'ANSI et qui correspond à environ 1 cycle/jour pendant 20 ans. Cette valeur est rarement atteinte dans les installations industrielles chimiques ou pétrochimiques. Le coefficient ( f ) est donné à la Fig 3-138
Remarque : Si l'amplitude des cycles de température varie, un nombre équivalent N de cycles complets de température peut être évalué comme suit:
N = NE + R15 x N1 + R25 x N2 + ........ + Rn5 x Nn ou NE = nombre de cycles de pleine amplitude DTE de température pour laquelle les contraintes d'expansion thermiques ont été calculées.
N1, N2, Nn = nombres de cycles respectifs de variations plus faibles de température DT1, DT2,....DTn
R1, R2, .... Rn =
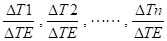
Pour l' ANSI B31.3, l'équation imposée est similaire, mais sous une autre forme, à celle que nous venons de voir.
4. Origine de l'amplitude admissible des contraintes d'expansion thermiques adoptées par les codes ANSI
On le sait déjà , mais il n'est pas inutile de rappeler que la principale cause de rupture d'une tuyauterie est la fatigue. Il s'agit de fatigue à bas nombre de cycles et donc, dans ce cas, la résistance est moins sensible à la valeur de la contrainte moyenne. Celle-ci est d'ailleurs difficilement déterminable surtout lorsqu'il y a relaxation. Toute l'analyse du code ANSI se base sur l'amplitude de contrainte produite par une précontrainte de 100%, soit SE ( FIG 3.104 b ).
Si ( Sr ) est la contrainte à chaud après stabilisation de la relaxation, cette contrainte devient à froid:
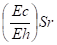
Sc" = SE -
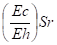
Dans ce cas, les amplitudes de contrainte réelle valent:
Sc' + Sh' = C . SE ( 1 - C )
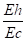
C = taux de précontrainte ( max C = 1 , en général C = 0,5 )
- Après relaxation complète : Sc" + Sh" = SE -
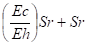
Les codes adoptent pour limites de ces amplitudes de contrainte:
- Tuyauteries à faible température ( Eh » Ec )
Sc' + Sh' = SE
Sc'' + Sh'' = SE
- Tuyauteries à température élevée ( 400 à 500°C ) en supposant Eh » 2 Ec / 3
Sc' + Sh' =
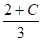
Sc'' + Sh'' = SE - Sr / 2 £ SE
Contrairement au cas des tuyauteries à faible température, l'amplitude de la contrainte dans le cas des tuyauteries à température élevée n'est pas constante et liée à ( C ) et à ( Sr ).
Etant donné qu'il n'est pas possible de prédire la valeur de ( Sr ) surtout lorsque celle-ci résulte de sollicitations par flexion ( cas général en tuyauterie ), les codes ANSI adoptent Sr » 1,6 Sh , ce qui correspond à 1,6 fois la valeur de la contrainte entraînant un allongement par fluage de 0,01% en 1000 heures, avec comme maximum la valeur de la limite élastique à la température de calcul. De même, il y a lieu de limiter Sc' et Sc'' à 1,6 Sc afin d'éviter les déformation permanentes à froid. Dés lors, on pourrait admettre comme amplitude maximale de fluctuation de la contrainte en un point du système :
1,6 ( Sh + Sc )
Sur ces bases, les codes ANSI ont finalement adopté pour amplitude maximale des seules contraintes dues à l'expansion thermique:
SA = f ( 1,25 Sc + 0,25 Sh )
Ce qui, dans le cas maximum pour f = 1, devient lorsque l'on prend également en compte les autres contraintes longitudinales dues au poids et à la pression:
SA = 1,25 ( Sc + Sh )
Rappelons que f tient compte de la réduction de la contrainte en fatigue en fonction du nombre de cycles N selon la loi : f . N0,2 = 6
Remarques : PIPEPLUS de ALGOR © dans son report stress calcul ou via la fonction graphique INQUIRE indique les valeurs suivantes :
- La contrainte radiale dite primaire (HOOP) : SH = p
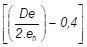
- La contrainte longitudinale SL ( voir § 3.5.3.2 )
- La contrainte principale Sp =
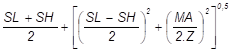
- La contrainte dite « code » : SC = SE + f . SL ( SE définit au § 3.5.3.3 et SL au § 3.5.3.2 ). Notons que pour déterminer SL, il faut établir un cas combiné avec pression + poids mort et pour SE un cas avec uniquement la température.
Pour satisfaire aux codes ANSI et EN 13480, il faut combiner les cas de charges comme suit :
CC1 : Pression + poids mort et autres charges + thermique + déplacements (ancrages avec déplacements imposés) afin de satisfaire l'équation 12A de l'ANSI ou 12.3.3-1 de EN 13480.
CC2 : Pression + poids mort pour satisfaire l'équation 11A de l'ANSI ou 12.3.2-1 de EN 13480.
CC3 : Température pour satisfaire l'équation 13A de l'ANSI et 12.3.4-1 de EN 13480. Mais ce cas n'a d'intérêt que pour vérifier SC étant donné qu'il y a toujours une masse gravitaire associée à une tuyauterie.
CC4A : Le CC1 + séisme ou le CC1 + vent normal suivant une direction horizontale.
CC4B : Idem mais seisme ou vent suivant l'autre direction horizontale.
A noter que tous les logiciels de calcul des tuyauteries procèdent de la même façon.
Dernière édition:






