Forces dues au passage du fluide dans les tuyauteries

[rocdacier]

4.4.3 FORCES PROPRES AU PASSAGE DU FLUIDE DANS LES TUYAUTERIES

1) Forces de dilatation : Elles ne sont pas absorbées par le compensateur. Les contraintes longitudinales sur la tuyauterie peuvent atteindre des valeurs considérables comme nous l′avons déjà  indiqué au § 2.2.2. Rappel : P =

= Newton

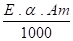
E = Module d′élasticité ( de YOUNG )
N/mm²

Am = section métallique de la

tuyauterie = mm²

a = élongation de la matière( mm/m )

DL = L . a

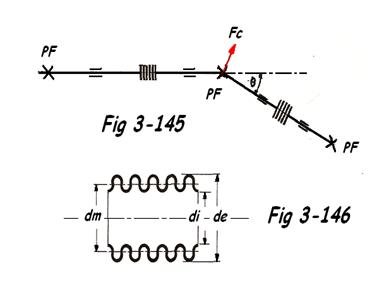
2) Force centrifuge dans les coudes : Selon la vitesse de passage du fluide, elle est plus ou moins négligeable, sauf dans le cas d'un fluide a masse volumique élevée ayant une grande vitesse d'écoulement.
Fc =

= Newton

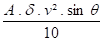
A = section efficace du soufflet donnée dans les catalogues ou en adoptant, en première approximation :

A =

= cm² avec dm = 0,5 ( di + de ) = cm

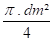
δ = masse volumique du fluide g/cm³

v = vitesse d'écoulement du fluide m/s

θ = angle de la tuyauterie ( ou du coude ) en degrès.

3) Forces et éléments associés aux compensateurs et tuyauteries

- Effet de fond: L′introduction d′un compensateur avec soufflet libre, dans un tronçon droit de tuyauterie, donne systématiquement un effet de fond sur les points d′ancrage ( points fixes ) situés à  chaque coin du tronçon à  compenser.

Quel que soit le nombre de compensateurs placés sur un tronçon droit, l′effet de fond résultant est le même que pour un seul compensateur. Il a pour expression:

Fs =

= Newton

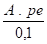
A = section efficace du soufflet = cm²

pe = pression d′épreuve ou pression de calcul selon le cas ( barg )

Si la pression interne est supérieure à  la pression externe, le compensateur sans points fixes serait allongé sous l′effet de la pression. A l′inverse, le compensateur serait comprimé, lorsque l′on réalise des épreuves hydrauliques par section d′un système complexe de tuyauteries sans disposer de joints fixes importants aux extrémités, les compensateurs doivent être ‘′ bridés ‘′ au moyen de tiges filetées par exemple.

4) Forces de déplacement des compensateurs

Elles sont fonction de la raideur du soufflet et des dilatations ou contractions thermiques de la tuyauterie à  compenser.

Les raideurs d′un compensateur ( axial, radial ) sont indiquées dans les tables de dimensions des fabricants et sont parfois qualifiées de coefficient de déplacement ( Cr, Cp, Cl, CD, Ca ) et sont mentionnés exclusivement à  froid. Ces valeurs doivent être corrigées par un coefficient en fonction de la température. ( coefficients indiqués pour l′AISI 321 et l′INCOLOY )

t° de calcul <200°C 200 300 400 500 600 700 800 900

Coef. réduc 1 0,93 0,9 0,86 0,83 0,81 0,79 0,77 0,75

( Kd )

Quelle que soit la raideur C = C(i) x Kd

C(i) = coefficient de déplacement ( raideur ) donnée dans le catalogue

C = coefficient final tenant compte de la température

Il est possible de déterminer les diverses raideurs par la résistance des matériaux, mais cela dépasserait le cadre de cet ouvrage qui doit rester simple et pratique. Nous renvoyons le lecteur intéressé au CODAP 95 ou à  l'EJMA ou encore à  l′ouvrage de M. J. LECOMTE ‘′ Chaudronnerie et tuyauteries industrielles " aux éditions TEC & DOC LAVOISIER ( France ).

Remarque :Il faut savoir que la raideur d′une onde CD
représente la force axiale qui est nécessaire pour la compression ( ou l′extension ) de l′onde de la valeur unitaire du déplacement ( N/mm ) . Cette valeur est généralement communiquée par le fabricant et est essentiellement fonction du coefficient de forme qui définit sa flexibilité.

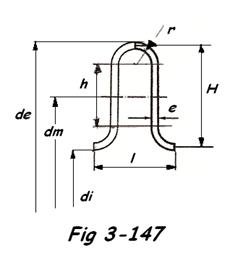
En l′absence de cette donnée, ce qui est généralement les cas dans une près-étude, La société KELLOGG propose une formule permettant de prédéterminer cette valeur pour une onde en U ( FIG 3-147 ).

CΔ =

avec h = H - 2 r

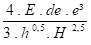
e = eps de l′onde (mm)

de = diam. ext de l′onde (mm)

H = hauteur de l′onde (mm)

r = rayon de cintrage (mm)

E = module d′élasticité à  la t° de calcul ( N/mm² )

a) Compensateurs axiaux

Effort sur points fixes extrêmes fD = CD .

= Newton avec précontrainte de 50%

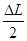
CD= raideur axiale éventuellement affectée du coefficient Kd ( N/mm )

DL = allongement total à  absorber

Aux coudes: fD= CD x DL x sin q/ 2 avec précontrainte de 50%

b) Compensateurs latéraux

Force de déplacement dues à  la position de déviation totale

fr= Cr x Pc

fp = Cp x Pc x DL / 2 avec précontrainte de 50%

fl= Cl x DL / 2 ‘′ ‘′ ‘′ ‘′

Cr = raideur due à  la friction de l′articulation en fonction de la pression de calcul ( N/bar )

Cp = raideur due à  la transmission de l′effort résistant du soufflet en fonction de la pression de calcul N/mm bar

Cl= raideur latérale du compensateur ( N/mm )

FL = fr + fp + fl

c) Compensateurs angulaires

Moment dus aux couples de raideur:

Mr = moment dû à  Cr : Cr x Pc

Ma= ‘′ ‘′ ‘′ ‘′ : Ca x a / 2 avec précontrainte de 50%

Mp = ‘′ ‘′ ‘′ ‘′ : Cp x Pc x a / 2 ‘′ ‘′ ‘′ ‘′

LA = longueur entre axes des soufflets

Nous détaillerons ces calculs au paragraphe 4.7.3 ( installation des compensateurs angulaires )

5) Forces de frottement sur les supports guides

Elles sont inhérentes à  la résistance des patins fixés sur la tuyauterie, glissant sur le support ( en général les poutrelles de racks ). Elles ont pour expression:

Fg = m x d x L = Newton

m = coefficient de frottement ( nombre sans dimension )

Exemples:
acier / acier : 0,2 à  0,5
acier / PTFE : 0,1 à  0,2
Paliers à  rouleaux : 0,05 à  0,1

d =masse linéique du tube ( N/m )

L = distance du compensateur au point fixe ( m )

​