


4.7.3 COMPENSATEURS ANGULAIRES
Les compensateurs angulaires ne sont sollicités qu′en flexion. Leurs articulations, dont les axes de pivotement sont dans le plan médian du soufflet, interdisent les variations de longueur du compensateur. Une compensation demande toujours que l'on place au moins deux éléments angulaires. Mais, en règle générale, l′agencement en montage articulé triple est préférable.
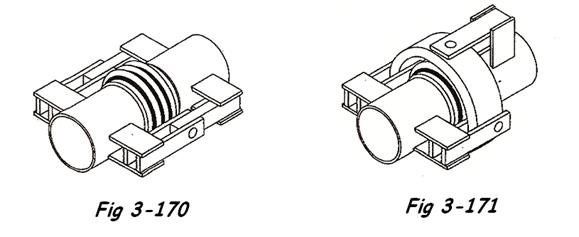
On trouve dans le commerce des compensateurs angulaires mobiles dans un seul plan ( FIG 3-170 ) comportant une articulation avec tourillon, ils ne peuvent être déformés qu'en flexion, mais aussi des compensateurs mobiles en tous sens ( compensateurs à cardan FIG 3-171 ) admettant des mouvements angulaires dans toutes les directions ( mouvement de rotule ). Ils sont surtout utilisés pour absorber les mouvements dans les systèmes tridimensionnels.
Le montage des compensateurs angulaires se fait de préférence à proximité des angles ( coudes ) ou changement de niveau de préférence à 90°, qui seraient présents dans le tracé de la tuyauterie. S'il n'y en a pas, le projeteur intégrera un aménagement en U ou un changement de niveau en L, par exemple.
Deux compensateurs angulaires correspondent fonctionnellement à un compensateur latéral, mais ils reviendront beaucoup plus cher.
D'une manière générale, il est possible de classer les systèmes de compensation comme suit:
- Systèmes à 2 articulations
- Systèmes à 3 articulations
- Systèmes à 3 articulations en U
- " " " en L
- " " " en Z
4.7.3.1 CALCUL DES SYSTEMES ARTICULES
a) Système à 2 articulations dans un plan
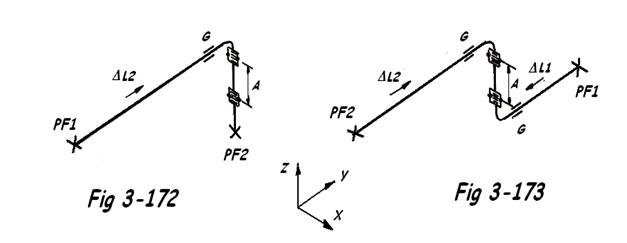
En général, on utilisera un compensateur latéral, sauf si le mouvement est important ( question de prix ). L'utilisation de deux compensateurs angulaires demande, au projeteur, de pouvoir déterminer la cote A ( distance entre tourillons des compensateurs ) comme indiqué aux Fig 3-172 et 173. Ces figures peuvent également être schématisées comme suit :
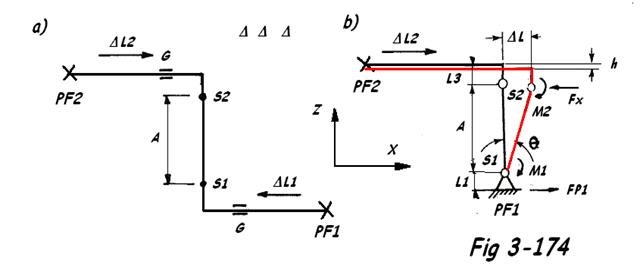
DL = mouvement résultant du système ( mm )
A = distance entre articulation des compensateurs ( mm )
q = angle de flexion entre compensateurs S1 et S2 ( ° )
DL = DL1 + DL2 ( FIG 3.174 a )
DL = DL2 ( FIG 3.174 b )
Pour une précontrainte de 50% Δx =
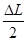
S'il faut tenir compte de la température en fin de montage Δx =
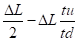
En général, la branche verticale offre une dilatation tout à fait négligeable.
L'angle de flexion est déterminé à partir de la relation q= arc sin
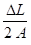
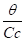
La hauteur de la flèche sera donnée par la relation h = A ( 1 - cos 2 q)
Cette diminution est donnée à la fois en position de précontrainte et de service. Si on y ajoute la dilatation thermique du coude, ces valeurs seront compensées par la flexion de la tuyauterie.
- Calcul des moments de compensateurs
M1 = Cr . Pc + Ca . q + Cp . Pc . q
M2 = M1 + M ( mN ou mdaN suivant le système d'unités utilisé )
Cr, Ca , Cp sont les raideurs angulaires données dans les tables de dimension des constructeurs.
- Calcul des forces au départ des moments
Fx =
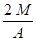
FP1 =
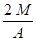
- Forces de frottement
Fg = µ . P . L
µ = coefficient de frottement appui / support ( 0,3 à 0,8 )
P = poids de la tuyauterie ( N )
L = longueur de la tuyauterie ( m )
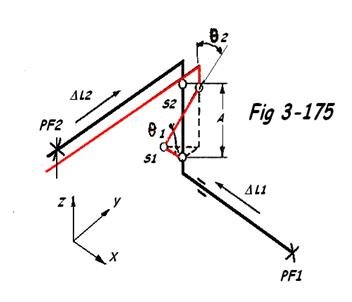
b) Système à 2 articulations dans l'espace
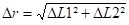
θr = θ1 = θ2 = arc sin
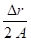
Pour une précontrainte de 50% afin de satisfaire au cahier des charges en fonction du nombre de cycles :
α0 =
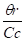
Δx =
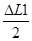
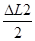
La distance A devra être prédéterminée par le projeteur. Sil fallait tenir compte de la température de montage, les précontraintes Δx et Δy seraient déterminées par les relations habituelles :
Δx =
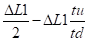
Δy =
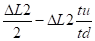
- Calcul des moments aux compensateurs
M1 = M2 = M = Cr . Pc + Ca . Pc . q
Cr, Ca, Cp sont les raideurs angulaires données dans les tables de dimensions des constructeurs.
- Calcul des forces à partir des moments
Fa1 =
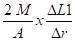
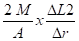
- Forces de frottement : Fg = µ . P . L pour chaque branche
- Effort total au point fixe PF2 : FP2 = Fa2 + ( µ . Fa1 ) + Fg2
- Effort total au point fixe PF1 : FP1 = Fa1 + ( µ . Fa2 ) + Fg1
c) Système à 3 articulations en U
On peut considérer le système en U comme étant la combinaison de 2 systèmes à 2 articulations.
Dans ce cas, les compensateurs situés au sommet du système en U sont regroupés en un seul compensateur. Il faudra prédéterminer les distances A et B entre les articulations, avec B choisie aussi courte que possible. En règle générale, B = 2 x rayon de courbure des coudes à 90° + la longueur totale des compensateurs S1 et S2 / 2 ).
- Mouvement résultant du système : Dr = ½ ( DL1 + DL2 )
- Calcul des paramètres auxiliaires: F = B -
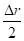
Le signe ( + ) est adopté en cas de contraction ou pour le calcul de l'angle exacte de précontrainte.
D =
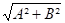
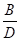
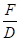
D D
- Angle de flexion: q1 = q2 = j1 - j2 q3 = 2 q1 (angle de flexion au sommet du compensateur S3)
- Hauteur de la flèche : h =
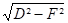
Il y a lieu, si cela est possible, de précontrainte le système U de 50%, les compensateurs travailleront ainsi sur les côtés avec un angle de flexion sensiblement identique autour de la position neutre.
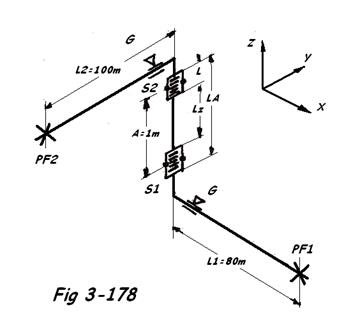
Moments des compensateurs au droit des raccordements:
M1 = Cr1 . Pc + Ca1 . q1 + Cp1 . Pc . q1 ( mN )
M2 = M1 ( si les compensateurs sont identiques )
M3 = Cr3 . Pc + Ca3 . q3 + Cp3 . Pc . q3 ( mN )
- Calcul des forces de déplacement ( Fx ) :
Fx =
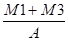
A = distance entre les articulations ( m )
- Calcul des forces exercées sur les points fixes : Mz = M1 = M2 ( si les compensateurs sont identiques ).
Exemples numériques
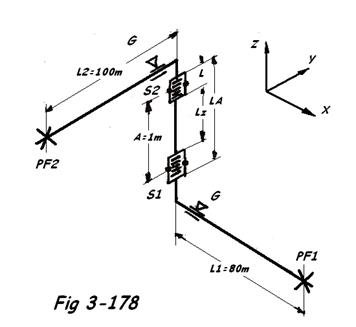
Soit une conduite ( dn 300 PN 16 ) véhiculant un fluide à la température de calcul de 130°C et à la pression de calcul de 12 barg.
Température minimale = -10°C. On demande de déterminer les efforts aux points fixes.
Δt = 130 - ( *10 ) = 140°C
Allongement pour 140°C = 1,7 mm/m
Cc = 0,99 ( 1000 cycles )
Cp = 0,82
μ1 = μ2 = 0,3 ( coef. De frottement )
Solution
ΔL2 = 100 x 1,7 = 170 mm
ΔL1 = 80 x 1,7 = 136 mm
Δr =
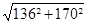
PF =
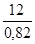
q = arc sin
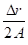
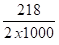
a0 =
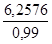
Le catalogue HYDRA nous donne 2aN = 14° soit +/- 7° > a0
Raideurs angulaires: Cr = 22,8 Nm / bar
Ca = 93 Nm / degré
Cp = 3,3 Nm / degré bar
Lz = A - 2 .
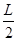
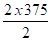
LA = 1000 +
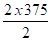
Précontraintes dans le cas ou la température de fin de montage est négligée
Δx =
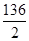
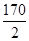
Note : En tenant compte de la température de fin de montage
Δx =
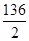
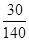
Δy =
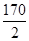
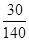
- Calcul des moments aux compensateurs
M1 = M2 = M = 22,8 x 12 + 3,3 x 12 x 6°321 + 9,3 x 6° 321 = 1135,5 mN
Fa1 =
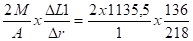
Fa2 =
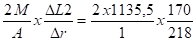
- Calcul des forces de frottement
Fg1 = 0,3 x 1250 x 80 = 30 000 N
Fg2 = 0,3 x 1250 x 100 = 37 500 N
- forces transversales sur les supports de part et d'autre des compensateurs
- Support situé sur la branche 2; l'effort est dû à Fa1 soit 1417 N
- Support situé sur la branche 1; l'effort est dû à Fa2 soit 1771 N
- Calcul des efforts aux points fixes PF1 et PF2
FP2 = Fa2 + Fa1 . µ1 + Fg2 = 1771 + 1417 x 0,3 + 37 500 = 39 691 N
FP1 = Fa1 + Fa2 . µ2 + Fg1 = 1417 + 1771 x 0,3 + 30 000 = 31 948 N
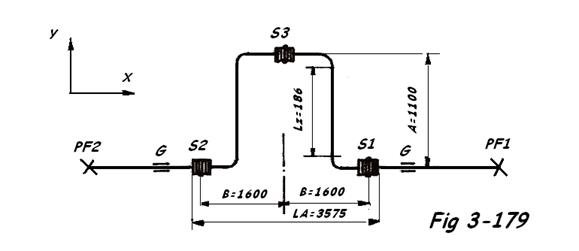
2) Montage articulé tripe en U ( dans un plan ) Fig 3-179
Nous reprendrons les mêmes conditions de calcul que dans le cas précédent
Solution
ΔL1 = ΔL2 = 1,7 x 80 = 136 mm
Δr =
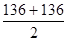
En première estimation, nous avons adopté des valeurs suivantes : A = 1100 mm et B = 1600 mm
D =
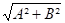
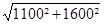
F = B - ½ . Δr = 1600 -
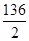
j1 = arc sin
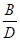
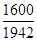
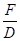
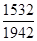
q1 = q2 = 55° 4764 - 52° 0807 = 3° 3957
a1 =
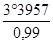
a3 = 2 a1 = 2 x 4 = +/- 8° soit 2 a3 = 16°
Du catalogue HYDRA, nous adopterons pour les compensateurs S1 et S2 : 2 aN1 = 14° ( 9° étant jugé trop juste ) et pour S3 : 2aN3 = 24°
Les tables de dimensions nous donnent pour S1 et S2: Cr1 = 22,8 Nm/bar ; Ca1 = 93 Nm/degré et Cp1 = 3,3 Nm/degré bar. Pour S3 nous aurons Cr3 = 22,6 Nm/bar ; Ca3 = 108 Nm/degré et Cp3 = 7,1 Nm/degré bar.
Lz = 1100 - 2 x 457 = 186 mm et La = 2 x 1600 + 375 = 3575 mm
Calcul de la précontrainte
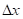
Δx =
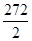
La différence entre cette valeur et celle obtenue par la méthode simplifiée n'est que de 136 - 129 = 7 mm qui est une valeur très négligeable.
Si nous devions tenir compte de la température de fin de montage:
Δx =
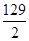
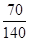
2 140
M1 = M2 = 22,8 x 12 + 3,3 x 12 x 4 + 9,3 x 4 = 469,2 Nm
M3 = 22,6 x 12 + 7,1 x 12 x 8 + 108 x 8 = 1816,8 Nm
Fx =
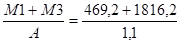
Forces dues au frottement : Fg = 0,3 x 1250 x 80 = 30 000 N ( à gauche ou à droite dans ce cas )
Efforts exercés sur les points fixes PF1 et PF2
FPa= Fx = 2077,6 N + 30 000 N = 32 077,6 N
Moments exercés sur les points fixes: Mpz = M1 = M2 = 469,2 Nm
d) Système à 3 articulations en L et Z ( en plan )
La compensation est assurée, même pour les mouvements d'amplitude maximale, sans qu'interviennent des contraintes de flexion dues à l'absorption de mouvements par élasticité naturelle dans les branches conjuguées comme dans le cas des systèmes articulés doubles.
Un tel montage requière souvent des calculs par approximations successives, mais qui se simplifient avec l'expérience du projeteur. En outre, on utilise souvent des compensateurs angulaires identiques. Il en résulte qu'en de nombreux endroits, l'angle de flexion disponible n'est pas complètement utilisé et que de ce fait des calculs plus précis ne sont évidemment pas indispensables en ces endroits.
Remarques: Les systèmes en Z ( Z1, Z2 ) peuvent être assimilés au système en L.
- D'une manière générale, pour les montages L et Z1, il est recommandé de monter 2 compensateurs angulaires sur la portion de tuyauterie ayant le plus petit mouvement et le troisième compensateur étant placé sur le tronçon ayant le mouvement le plus important.
- Les approches sont toutefois assez différentes pour le système Z2 ( FIG 3-182 ). Il est cependant recommandé d'adopter pour le compensateur S1 une faible déviation angulaire.
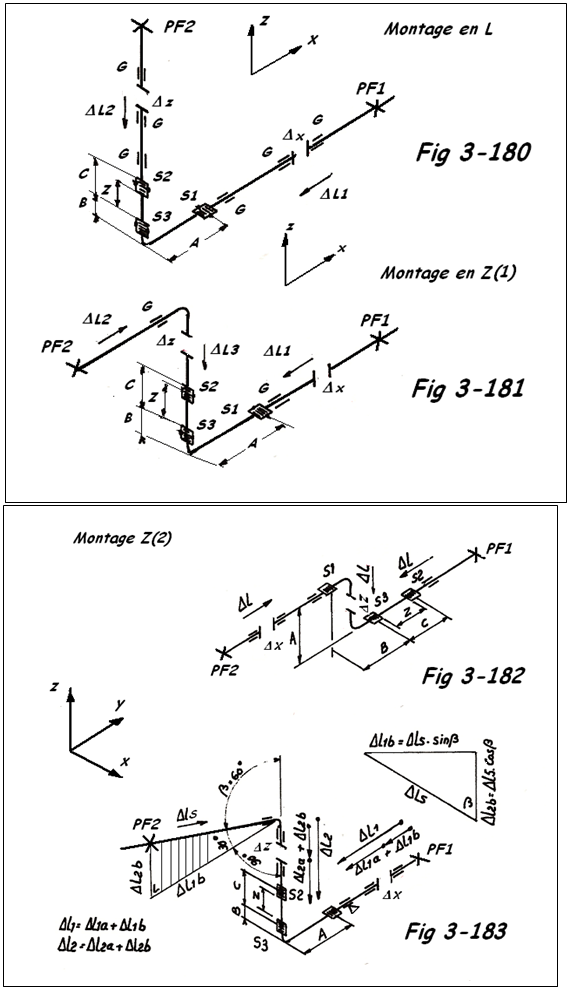
Une variante au montage Z1 est proposée à la FIG 3-183. L'une de ces branches est inclinée à 30° par rapport à l'horizontale. Le mouvement provenant de ce tronçon doit être décomposé selon 2 directions et nous aurons 2 composantes DL1 et DL2 que l'on additionne ensuite aux mouvements de directions correspondantes.
q2 = arc sin
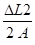
D'où A =
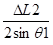
q2 = arc sin
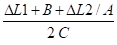
q2 = arc sin
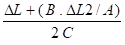
q3 = q1 + q2
ao = qn / Cc £aN ( Cc = coefficient global de longévité )
ΔL2 = A x 2 sin q1 et DL1 = C x 2 sin q2 - B
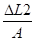
L'examen de ces formules montre que ( A ) sera d'autant plus petit que l'angle de flexion ( q) des compensateurs angulaires voisins sera grand et inversement.
La distance ( C ) dépend, pour l'essentiel , de l'angle de flexion des compensateurs angulaires voisins. mais de plus, elle dépend de la longueur ( B ) qui devra être la plus courte possible.
Si l'on ne doit pas tenir compte de la température de fin de montage, les précontraintes peuvent être calculées au départ des relations suivantes:
- Système en L Δx = DL1 / 2 et
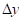
- Système en Z
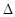
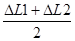
Si l'on désire un calcul plus rigoureux des précontraintes:
Δx = C x sin q2 - A ( 1 - cos q1 ) - B sin q1
Δy = A x sin q1 - B ( 1 - cos q1 ) - C ( 1 - cos q2 )
Et pour le cas où l'on doit tenir compte de la température de fin de montage, on utilisera la relation connue
Δx =
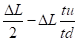
Exemples numériques:
1. Montage articulé triple en L ( dans un même plan )
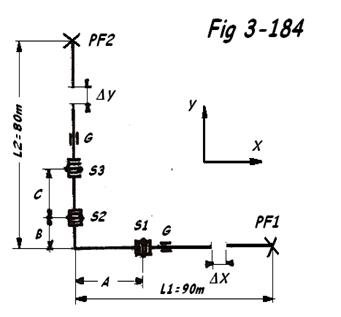
Reprenons toujours notre conduite dn 300, PN 16 véhiculant un fluide à la température de 130 °C, sous une pression de calcul = 12 barg. La température minimale = - 10°C.
Δt = 130 - (-10) = 140 °C.
Allongement pour 140 °C = 1,7 mm/m
D'après nos différents calculs précédents,
Cc = 0,99 ( 1000 cycles )
Cp = 0,82
μ1 = μ2 = 0,3 ( coefficient de frottement )
On demande de calculer les efforts aux points fixes PF1 et PF2.
A = 1400 mm ; B = 850 mm ; C = 1500 mm
Longueur d'un coude 3D = 457 mm.
Solution
DL1 = 90 x 1,7 = 153 mm
DL2 = 80 x 1,7 mm = 136 mm
q1 = arc sin
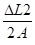
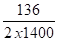
q1 = arc sin
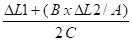
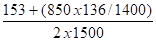
q3 = q2 + q1 = 2°,784 + 4°,503 = 7°, 287 => sin q3 = 0,12684
a1 =
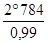
a2 =
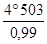
a3 =
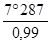
Dans les tables de dimensions du catalogue HYDRA nous pouvons choisir pour:
- S1 le type WRN16.0300.090.0 2 aN = 90° longueur = 340 mm
- S2 " " 0140.0 " = 14° " = 375 mm
- S3 " " 0240.0 " = 24'' " = 495 mm
D'où les coefficients de raideur:
Cr1 = 22,7 Nm/bar Ca1 = 151 Nm/degré Cp1 = 2 Nm/degré bar
Cr2 = 22,8 " Ca2 = 93 " Cp2 = 3,3 "
Cr3 = 22,6 " Ca3 = 108 " Cp3 = 7,1 "
Note: Les valeurs de Cp sont très faibles et parfois supprimées chez certains fabricants ou fournisseurs.
Précontraintes simplifiées: Δx = 153 / 2 = 76,5 mm et Δy = 136 / 2 = 68 mm
Un calcul rigoureux aurait donné: Δx = 1500 x 0,07851 - 1400 ( 1 - cos 4°,503 ) - ( 850 x sin 4°, 503 )
= 72,5 mm
Δy = 1400 x 0,048857 - 850 ( 1 - cos 4°, 503 ) - 1500 ( 1 - cos 4°,503 )
= 61 mm
On constate qu'il n'y a que quelques millimètres de différence entre les 2 résultats.
Note: S'il avait fallu tenir compte de la température de fin de montage:
Δx = 72,5 - 153
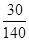
Δy = 61 - 136
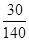
Calcul des moments dus par le compensateur:
M1 =22,7 x 12 + 151 x 2°,784 + 2 x 12 x 2,784 » 760 mN
M2 = 22,8 x 12 + 93 x 4°,503 + 3,3 x 12 x 4°,503 »871 mN
M3 = 22,6 x 12 + 108 x 7°,287 + 7,1 x 12 x 7°,287 »1680 mN
Calcul des forces de déplacement dues à la position de déviation.
F1 =
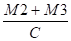
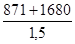
F2 =
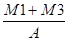
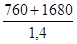
Calcul des forces de frottement
Tronçon de gauche Fg2 = 0,3 x 1250 x 80 = 30 000 N
Fg1 = 0,3 x 1250 x 90 = 33 750 N
Forces transversales sur les supports guides, de part et d'autre des compensateurs:
- Devant S1 : Ft1 dû à F2 = 1743 N
- Devant S2 Ft2 dû à F1 = 1701 N
Calcul des efforts sur les points fixes
Fpf2 = 1743 + ( 1701 x 0,3 ) + 30 000 » 32 254 N
Fpf3 = 1701 + ( 1743 x 0,3 ) + 33 750 » 35 975 N
2. Montage articulé en Z ( dans un plan )
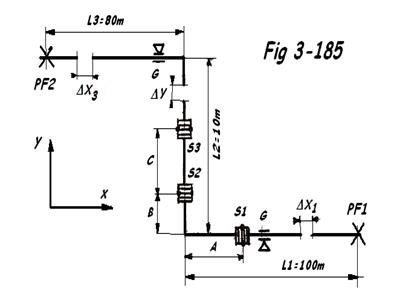
A = 1400 mm
B = 850 mm
C = 1500 mm
Coude 3D = 457 mm de rayon
Cc = 0,99
μ = 0,3
Cp = 0,82
Conditions de calcul : voir exemple 1.
Calculer les efforts aux points fixes.
Solution
DL1 = 100 x 1,7 = 170 mm
DL2 = 10 x 1,7 = 17 mm
DL3 = 80 x 1,7 = 136 mm
q1 =arc sin
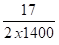
q2 =arc sin
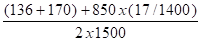
q3 = 0°,348 + 6°,0525 = 6°, 4005 soit 6° 24'
a1 =
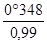
a2 =
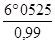
a3 =
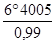
Nous pouvons maintenant choisir les compensateurs dans les tables de dimensions d'un constructeur
( ex: HYDRA )
S1 = type WRN16.0300-090-0 2aN = 90° longueur = 340 mm
S2 = " " " " " " = 240° "' = 495 mm
S3 = " " " " " " = " " = 495 mm
Ce qui nous donne les coefficients de raideur:
Cr1 = 22,7 Nm/bar Ca1 = 151 Nm/degré Cp1 = 2 Nm/degré bar
Cr2 = Cr3 = 22,6 Nm/bar Ca2 = Ca3 = 108 Nm/degré Cp2 = Cp3 = 7,1 Nm/degré bar
Calcul simplifié des précontraintes ( justifié dans ce cas ) Δx1 =
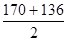
Δy = 17 / 2 = 8,5 mm
Nous ne ferons donc pas de calcul plus précis des précontraintes, du fait que nous avons adopté des compensateurs offrant un angle de flexion très grand rattrapant les imprécisions.
Calcul des moments des compensateurs:
M1 = 22,7 x 12 + 151 x 0°,348 + 2 x 12 x 0°,348 » 333, 3 mN
M2 = 22,6 x 12 + 108 x 6°,0525 + 7,1 x 12 x 6°,0525 = 1192 mN
M3 = 22,6 x 12 + 108 x 6°,4 + 7,1 x 12 x 6°,4 = 1508 mN
Calcul des forces de déplacement:
F1 =
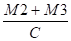
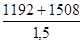
F2 =
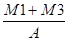
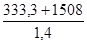
Calcul des forces de frottement
Fg1 = 0,3 x 1250 x 100 = 37 500 N
Fg2 = 0,3 x 1250 x 10 = 3750 N
Fg3 = 0,3 x 1250 x 80 = 30 000 N
Forces transversales sur les supports guides
Effort dû à F2 devant S1 = 1315 N
Effort dû à F2 + Fg2 devant S2 = 1315 + 3750 = 5065 N
Calcul des efforts sur les points fixes extrêmes:
Fpf2 = 1800 + ( 1315 x 0,3 ) + ( 3750 x 0,3 ) + 30 000 = 33 320 N
Fpf1 = 1800 + ( 1315 x 0,3 ) + ( 3750 x 0,3 ) + 37 500 = 40 820 N
q1 = arc sin
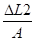
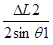
C =
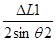
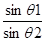
q‘2 = arc cos
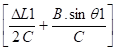
q"2 = arc cos
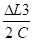
Cos q2 = cos q‘2 x cos q"2 ; q‘2 et q"2 ne peuvent être déterminés que par approximations successives.
q3 = arc cos ( cos ( q1 + q‘2 ) x cos q"2 )
Calcul des précontraintes
Δx1 = C sin q2 - A ( 1 - cos q1 ) - B sin q1
Δy = A sin q1 - B ( 1 - cos q1 ) + C ( cos q‘2 - cos q"2 )
Δx3 =
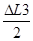
Dans de nombreux cas, on utilise les formules simplifiées :
Δx1 =
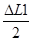
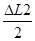
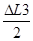
En cas ou il faut tenir compte de la température de fin de montage:
Δx1 =
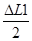
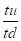
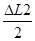
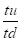
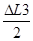
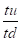
Calcul des moments des compensateurs
M1 = Cr1 x Pc + Ca1 x q1 + Cp1 x Pc x q1
M'2 = Cr2 x Pc + Ca2 x q‘2 + Cp2 x Pc x q‘2
M''2 = Cr2 x Pc + Ca2 x q"2 + Cp2 x Pc x q"2
M'3 = Cr3 x Pc + Ca3 x q‘3 + Cp3 x Pc x q‘3
M''3 = Cr3 x Pc + Ca3 x q"3 + Cp3 x Pc x q"3
Calcul des forces de déplacement
F1 =
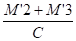
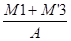
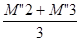
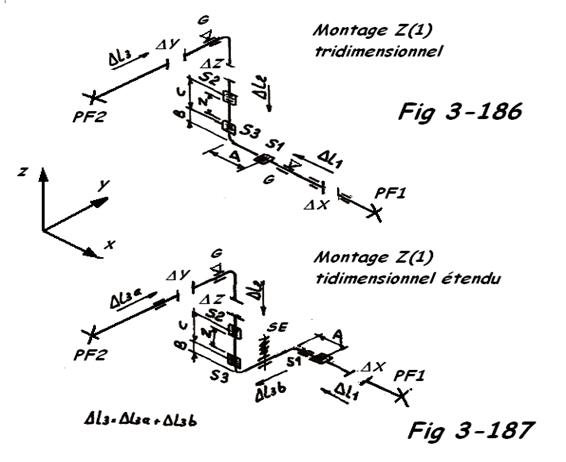
Note : Les compensateurs S2 et S3 sont à cardan, le compensateur S1 ne travaille que dans un plan, il est placé sur le tronçon ayant le mouvement le plus important.
Forces de frottement : Fg = m x P x L à calculer pour chaque tronçon
Calcul des efforts sur les points fixes
- Point fixe PF2 : Fpf2 = F3 + ( F2 x µ2 ) + ( F1 x µ1 ) + ( Fg2 x µ2 ) + Fg2
- Point fixe PF1 : Fpf1 = F1 + ( F2 x µ2 ) + ( F3 x µ3 ) + Fg1
e) Systèmes à 3 articulations en Z
Il est possible, ici, d'absorber des mouvements dans les 3 plans et on peut être assuré d'une parfaite compensation, même dans le cas de mouvements très importants. De plus, il n'y a pas de contrainte de flexion dues à l'absorption de mouvements par élasticité naturelle de banches conjuguées comme dans le cas des systèmes articulés doubles.
Toutefois, ce genre de montage demande une bonne expérience d'ingénierie dans ce domaine, afin de limiter les calculs par approximations successives.
Généralement et pour une raison d'opportunité, il est d'usage d'utiliser des compensateurs identiques par exemple dans le but de limiter les stocks en magasin. de ce fait, l'angle de flexion n'est pas complètement utilisé à de nombreux endroits et il devient inutile de procéder à des calculs très précis.
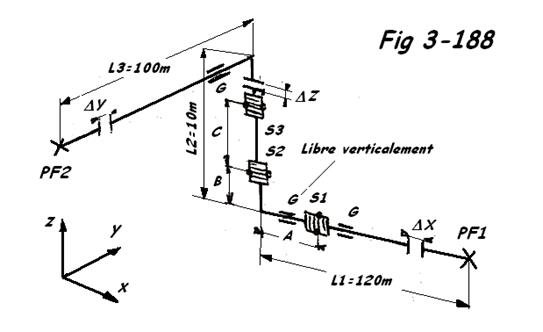
Exemple numérique ( Fig 3-188 )
A = 1400 mm ; B = 850 mm ; C = 1500 mm
Coude 3D : r = 457 mm
Cc =0,99 ; μ = 0,3 et Cp = 0,82
Conditions de calcul identiques aux exemples précédents. Calculer les efforts aux points fixes.
Solution
ΔL1 = 120 x 1,7 = 204 mm
ΔL2 = 10 x 1,7 = 17 mm
ΔL3 = 100 x 1,7 = 170 mm
Calcul des angles de flexion
q1 = arc sin
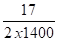
q‘2 = arc sin
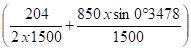
q"2 = arc sin
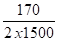
cos q"2 = 0,9984 ; cos q‘2 = 0,9975 ; cos q1 = 0,9999
q2 = arc cos ( 0,9975 x 0,9984 ) = 5° 1876
q‘3 = arc cos ( 0,9999 x 0,9975 ) x 0,9984 = 5° 2503
q"3 = q"2 = 3° 2485
Angle de flexion à adopter pour le calcul de M'3: q1 + q‘2 = 0,3478 + 4,097 » 4° 445
a1 =
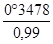
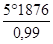
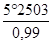
Choix des compensateurs angulaires ( d'après le catalogue HYDRA )
S1 = type WRN16.0300.090.0 2aN = 9° Longueur = 340 mm
S2 = " " " 140.0 ‘‘ = 14° " = 375 mm
S3 = " ‘‘ " " " = 14° " = 375 mm
Coefficients de raideur tirés des tables de dimensions
Cr1 = 22,7 Nm/bar Ca1 = 151 Nm/degré Cp1 = 2 Nm/degré
Cr2 = 22,8 " Ca2 = Ca3 = 93 " Cp2 = Cp3 = 3,3 Nm/degré
Calcul des forces transversales sur les supports guides de part et d'autre des compensateurs.
- Devant S1 due à F2 = 854,5 N
- Devant S2 due à F2 + Fg2 = 854,5 + 3750 = 4604,5 N
Sur le support guide transversal ( entre S1 et S3 ) = F3 = 939,5 N
" " " " ( au-dessus de S2 ) = 1120 N = F1
Le support guide transversal inférieur est recommandé car en son absence la force F1 devrait se manifester au-delà du compensateur S1. Le support guide transversal supérieur protège le tronçon 3 contre la torsion.
Calcul des forces sur les points fixes.
- Point fixe PF2 : Fpf2 = F3 + ( F2 x µ2 ) + ( F1 x µ1 ) + ( Fg2 x µ2 ) + Fg3
Fpf2 = 939,5 + ( 854,5 x 0,3 ) + ( 1120 x 0,3 ) + ( 3750 x 0,3 ) + 37 500
Fpf2 = 40 157 N
- Point fixe PF1 : Fpf1 = F1 + ( F2 x µ2 ) + ( F3 x µ3 ) + Fg1
Fpf1 = 1120 + ( 854,5 x 0,3 ) + ( 939,5 x 0,3 ) + 45 000
Fpf1 = 46 658 N
Dernière édition:







