


4.7.2 COMPENSATEURS LATERAUX
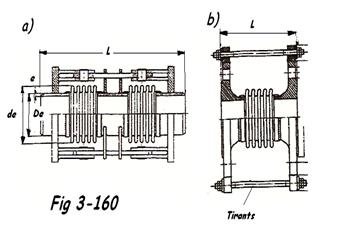
Les compensateurs simples peuvent dans certaines conditions, absorber une déflection latérale de faible amplitude. pour des amplitudes plus importantes, on peut utiliser des compensateurs ‘′ Universels ‘′ constitués de 2 soufflets réunis entre-eux par un tube intermédiaire. A l′état libre, nous savons que tout soufflet introduit un effet de fond. Pour éviter ce problème, on utilise des tirants montés sur des rotules ( pour les amplitudes latérales moyennes ) ou des articulations ( pour les grandes amplitudes ).
En outre, lorsque l'on réalise une compensation latérale, il subsiste un allongement résiduel devant être compensé par la flexibilité de la tuyauterie. Cet allongement est fonction de la dilatation ( ou contraction ) du tronçon non compensé, ainsi que de la hauteur de la flèche ( h ) due au mouvement circulaire du compensateur latéral ( Fig 3-161 ).
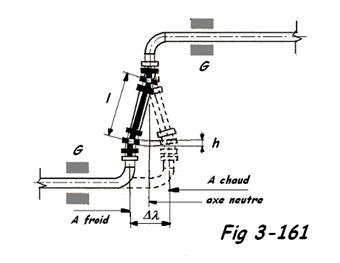
l = distance entre les articulations mm
Δλ = course latérale mm
h = l -
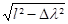
Il est donc nécessaire que l'appui guide ( G ) puisse reprendre la valeur de h, afin de ne pas empêcher l'allongement résiduel.
Le plan de glissement des appuis doit toujours être perpendiculaire aux axes de rotation des compensateurs.
Remarque: Lorsque des charges importantes sont appliquées au système, dans tous les plans, il est nécessaire de prévoir des suspensions ou des appuis élastiques, comme indiqué aux Fig 3-162, 163 et 164.
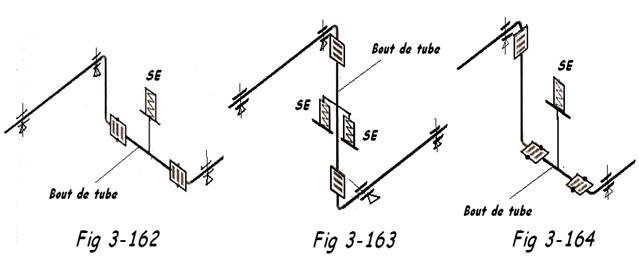
N.B : Comme dans tous problèmes de compensateurs, c′est à l′ingénierie de subdiviser correctement et supporter la tuyauterie, afin que les compensateurs puissent travailler au maximum de leurs possibilités.
1) Course latérale résultante dans le cas de mouvements dans l′espace
Les tables de dimensions des divers constructeurs indiquent les courses latérales nominales pour des déviations symétriques ( Δλ = 2 x
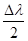
Δr =
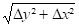
Dr = Course latérale résultante ( mm )
Dy = ‘′ ‘′ dans la direction principale ( mm )
Dx = ‘′ ‘′ ‘′ ‘′ ‘′ transversale ( mm )
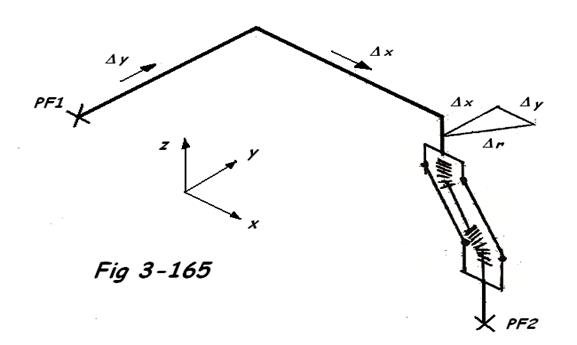
2) Prise en compte de la température de fin de montage
Lorsque cette température est sensiblement supérieure à la température minimale de calcul et que dans le même temps la température maximale est plus élevée, la contrainte initiale est déduite de la relation
Δx =
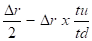
tu = te - tmin et td = tmax - tmin ( voir compensateurs axiaux )
Exemple: tmax = 130°C tmin = - 10°C te = 20°C
Dr = 216 mm ( contrainte de 50% )
Δx =
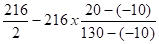
Le compensateur sera donc dévié de 62 mm de sa position rectiligne, en direction opposée au déplacement attendu de la tuyauterie.
3) Exemples numériques
a) Soit une conduite dn 200 PN 16 soumise à une pression de calcul de 12 barg, supportant une température maximale de calcul = -10°C.
Allongement du tube à 140 °C = 1,7 mm/m ( Δt = 130 - (-10) = 140°C )
Le compensateur sera garanti pour cycles
Le poids au mètre linéaire de la tuyauterie = 650 N/m.
Solution
ΔL = 80 x 1,7 = 136 mm
Cp = 0,82 pour Δt = 140 °C
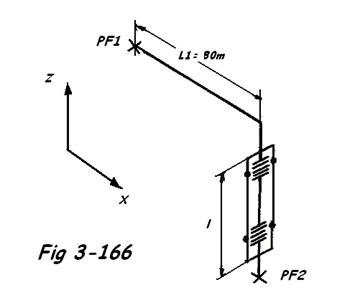
Pf =
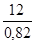
C1 = 0,96 ; pour Cp = 0,82 => C2 = 1,03
C3 = 1 pour 1000 cycles.
Cc = 0,96 x 1,03 x 1 = 0,99 < 1,15
Δx =
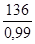
Le catalogue HYDRA donne dans ses tables de dimensions, un compensateur PN 16 ayant une longueur hors tout de 940 mm et une course latérale nominale de 150 mm > 136 et offrant les raideurs suivantes: Cr = 36 N/bar
Cp = 0,45 N/mm bar ; Cl = 20 N/mm
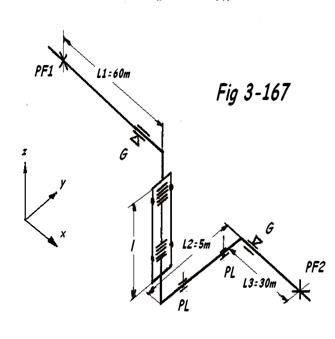
Note: En cas de calcul serré, la précontrainte à prendre en compte tenant compte de la température de fin de montage serait:
Δx =
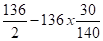
- Calcul des forces de déplacements
Fr = Cr x Pc = 36 x 12 = 432 N
Fp = Cp x Pc x ΔL/2 = 0,45 x 12 x 136/2
Fp = 367, 2 N
FL = 432 + 367,2 + 1360 = 2159,2 N
- Calcul de la force de frottement
Fg = 0,3 x 650 N/m x 80 m = 15600 N
- Calcul de l'effort sur les points fixes extrêmes
FPF = FL + Fg = 2159,2 + 15600 = 17759,2 N
b) Reprenons la tuyauterie dn 200 PN 16 soumise aux mêmes conditions physiques que dans l'exemple précédent et calculons les efforts aux points fixes.
Solution
ΔL1 = 60 x 1,7 = 102 mm
ΔL2 = 5 x 1,7 = 8,5 mm
ΔL3 = 30 x 1,7 = 51 mm
Dr =
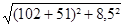
Cp = 0,82 ( Dtc = 140°C )
Pf = 12 / 0,82 = 14,6 barg < 16
C1 = 0,96 ; C2 = 1,03 ; C3 = 1 ( 1000 cycles )
Cc = 0,96 x 1,03 x 1 = 0,99 < 1,15
Δλ =
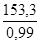
Le catalogue HYDRA indique de prendre un compensateur latéral ayant une longueur LR = 1150 mm permettant un mouvement latéral nominal de 200 mm > 155.
Précontrainte à réaliser normalement, c′est-à -dire lorsque la température en fin de montage est négligeable.
Δx =
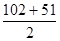
Il est inutile de prévoir une précontrainte pour le petit mouvement de 8,5 mm de la partie médiane.
Note: En cas de calcul tenant compte de cette température en fin de montage.
Δx =
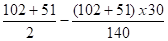
- Calcul des forces de déplacement
Fr = 30 x 12 = 360 N
Fp = 0,22 x 12 x
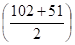
Fl= 11 x
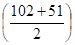
FL = 360 + 202 + 841,5 = 1403,5 N
Les forces de déplacement dues au mouvement de la branche médiane de m sont négligeables.
- Calcul des forces de frottement
- Pour la partie de gauche
Fg = 0,3 x 60 x 650 = 11700 N
- Pour la partie de droite
Fg = 0,3 x ( 30 + 5 ) x 650 = 6825 N
- Calcul des efforts sur les points fixes extrêmes ( PF1 et PF2 ).
FPF1 = 1403,5 + 11700 = 13103,5 N
FPF2 = 1403,5 + 6825 = 8228,5 N
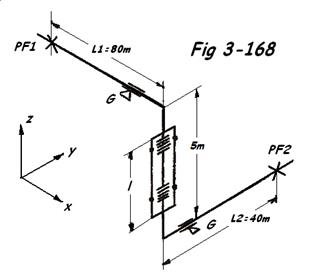
c) Nous adopterons toujours la même tuyauterie dn 200 PN 16 soumises aux mêmes conditions que dans les exemples précédents ( FIG 3-168 )
Solution
DL1 = 80 x 1,7 = 136 mm
DL2 = 40 x 1,7 = 68 mm
Dr =
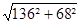
Cp = 0,82 ( Dtc = 140°C )
C1 = 0,96 ; C2 = 1,03 ; C3 = 1 ; Cc = 0,99 < 1,15
Δλ =
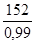
Nous adopterons le même compensateur que dans l′exemple 2. Mouvement latéral nominal = 200 mm
Δx = 136 / 2 = 68 mm
précontraintes
Δy = 68 / 2 = 34 mm
Note: S′il avait fallu tenir de compte de la température de fin de fin de montage:
Δx = 136 / 2 - 136 x
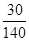
Δy = 68 / 2 - 68 x
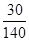
- Calculs des forces de déplacement pour le mouvement principal
Fr = 30 x 12 = 360 N
Fp = 0,22 x 12 x 136 / 2 = 179,6 N
Fl= 11 x 136 / 2 = 748 N
FL1 = 360 + 179,6 + 748 = 1287,6 N
- Calcul des forces de frottement
- Pour la partie gauche
Fg1 = 0,3 x 80 x 650 = 15 600 N
- Pour la partie droite
Fg2 = 0,3 x 40 x 650 = 7 800 N
- Calcul des efforts sur les points fixes PF1 et PF2
FPF1 = FL1 + ( FL2 x µ ) + Fg1
àŸ pour tenir compte du frottement de la branche de droite
FPF1 = 1287,6 + 823,76 x 0,3 + 15 600 = 17 135 N
FPF2 = 823,76 + 1287,6 + 7800 = 9 010 N
d) Nous adopterons à nouveau la même tuyauterie dn 200 PN 16 toujours soumises aux mêmes conditions que dans l′exemple a)
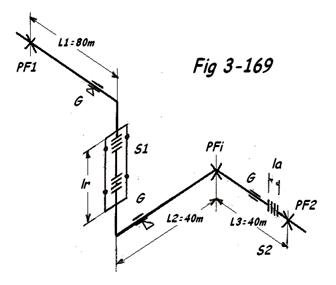
Solution
ΔL1 = 80 x 1,7 = 136 mm
ΔL2 = ΔL3 = 40 x 1,7 = 68 mm
- Compensateur S1
Δr =
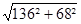
- Compensateur S2
ΔL3 = 68 mm
Cp = 0,85 ( Δt = 140 °C ) ; C1 = 0,96
C2 = 1,03 ; C3 = 1 ( 1000 cycles )
S1 : Δλ =
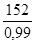
S2 : Δλ =
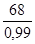
Dans la table de dimensions des compensateurs HYDRA , nous choisirons un compensateur offrant un mouvement latéral nominal de 200 mm > 154 mm ( S1 ). Dans le cas du compensateur axial ( S2 ) nous choisirons un mouvement axial nominal de 90 mm > 69.
Précontrainte dans le cas normal ( températurede fin de montage négligeable )
Compensateur S1 : Δx =
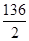
Δy =
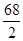
Compensateur S2 Δx =
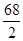
Note: En cas de prise en compte de la t° de fin de montage
Compensateur S1 ( mouvement principal )
Fr = 30 x 12 = 360 N
Fp = 0,22 x 12 x 136 / 2 = 179,5 N
Fl= 11 x 136 / 2 = 748 N
( Cr, Cp, Clsont tirés des tables de dimensions du constructeur des soufflets )
FL1 = 360 + 179,5 + 748 = 1287,5 N
Compensateur S1 ( mouvement transversal )
Fr = 30 x 12 = 360 N
Fp = 0,22 x 12 x 68 / 2 = 89,75 N
Fl= 11 x 68 / 2 = 374 N
FL2 = 360 + 89,75 + 374 = 823,75 N
Compensateur S2
FD= CD x DL3 / 2 = 226 x 68 / 2 = 7 684 N
CDest tiré des tables de dimensions du constructeur du soufflet
Calcul des forces de frottement
- branche de gauche Fg1 = 0,3 x 80 x 650 = 15 600 N
- ‘′ médiane Fg2 = 0,3 x 40 x 650 = 7 800 N
- ‘′ de droite Fg3 = 0,3 x 40 x 650 = 7 800 N
Effort sur guide placé avant S1 sur branche principal: FL = 823,75 N
Effort sur guide placé après S1 sur branche médiane : FL = 1287,5 N
Effort sur guide placé avant S2 : FL = 0
Calcul des efforts sur les points fixes ( PF1, PF2 )
- Point fixe PF1
FL = 1287,5 N
FL′ = 0,3 x 823,75 = 247,125 N ( accroissement de frottement )
Fg = 15 600 N
FPF1 = 1287,5 + 247,125 + 15 600 » 17 135 N
Calcul des efforts sur le point fixe intermédiaire( Pfi ) dû à la branche de droite
FL = 7 684 N
Fg = 7 800 N soufflet axial
Fp =
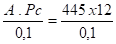
A = section efficace du soufflet tirée des tables de dimensions du constructeur
FH = 7 684 + 7 800 + 53 400 = 61 864 N
Calcul des efforts sur le point fixe PF2
FL = 7 684 N
Fp = 53 400 N
FL = 7 684 + 53 400 = 61 084 N
Dernière édition:






