


3.2.5 INTENSIFICATION DES CONTRAINTES ( FIG 3-100 )
Suite tableau FIG 3-100 : Réduction à souder en bout
Forgées ( normalisées ) K = 1,3 et i = 2 ( max )
Chaudronnées K = 2,16 « «
Les contraintes dans les coudes et les tubes cintrés provoquées par des moments externes de flexion et de torsion sont supérieurs à ce quelles seraient dans un tube droit soumis aux mêmes sollicitations et ce, d'autant plus que le rayon de cintrage est petit. De même, les contraintes dues aux déformations d'ensemble de la tuyauterie sont intensifiées dans toutes les pièces de connexion ( Tés, réductions, raccords, brides,... ) comme le montre le tableau FIG 3-100 et ce, d'autant plus que les angles de raccordement sont acérés. On peut même constater une intensification des contraintes dans les soudures bout à bout des tubes. Ces intensifications de contraintes sont importantes du point de vue risque d'inadaptation inélastique (coudes, courbes, ... ) ou de rupture par fatigue (autres cas ).
Remarque : Le coefficient d'intensification de contrainte ( i ) caractérise donc un niveau de résistance et le coefficient de concentration représente l'évaluation d'une contrainte réelle qui peut se vérifier si des mesures au moyen de jauges de contraintes sont effectuées. Il existe une relation entre ces 2 termes, mais elle est très complexe et difficile à déterminer. En pratique on peut considérer que K = 2 x i .
Exemple: Calcul d'une lyre symétrique telle que représentée à la FIG 3-106.
Données : Tube dn 200 ( 219,1 x 8 )
I (tube ) = 2959,6 cm4
I/v " = 270,161 cm3
E = 210 000 Mpa ( N/mm² )
L = 1 m ; R = 1 m ; H = 6 m et Dx = 100 mm.
Problème : Calculer la contrainte maximale
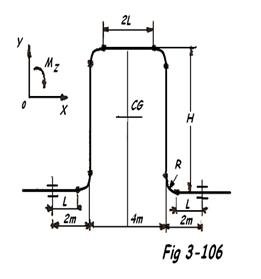
- Vu la symétrie de la lyre par rapport aux axes OY et OX, la force Fx est donnée par la relation :
Fx =
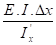
I'x =
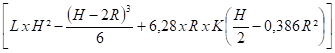
Pour un coude h =
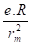
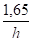
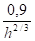
Note : On considère qu'au vu de h et K, un coude à 90° intervient dans le calcul avec une longueur fictive égale à
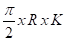
E.I . Δx = 210 E +9 N/m² x 2,9596 E -5 x 0,1 = 621516
h =
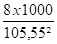
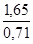
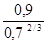
I'x =
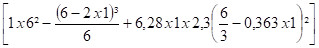
Fx =
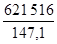
Mz =
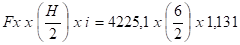
s =
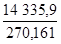
Dernière édition:






