


3.3 METHODES DE CALCULS APPROCHEES
Avant l'apparition du super calculateur qu'est l'ordinateur et des logiciels spécialisés, il existait de nombreuses méthodes simplifiées permettant d'alléger la tâche du projeteur. Même actuellement, l'expérience montre que ces méthodes ( Poutres encastrées, formule de l'ANSI, méthode de Carlier,... ) n'ont pas été totalement abandonnées, car elles permettent souvent d'éviter l'exécution de calculs coûteux qui en fin de compte, pourraient se révéler inacceptables. Très souvent, l'utilisation d'une de ces méthodes sera suffisante pour permettre de justifier le choix d'un tracé, en particulier pour les lignes simples, dont le critère d'acceptation n'est pas les efforts sur les machines tournantes par exemple.
3.3.1 METHODE DE LA POUTRE ENCASTREE
Cette méthode est basée sur l'analogie d'un tronçon de tuyauterie avec une poutre encastrée à ses 2 extrémités comme en R.D.M. et dont l'une de ses extrémités subit un déplacement perpendiculaire à l'axe de la poutre. Cette méthode est très pessimiste et peut conduire, dans certains cas, à un allongement inutile des tracés. Mais elle reste intéressante en tant que méthode de prédétermination ou pour les calculs des tuyauteries de petits diamètres.
L'application correcte de cette méthode impose quelques conditions:
- La tuyauterie doit être à 2 ancrages de même diamètre et de même épaisseur, sur toute sa longueur.
- Les tronçons doivent être parallèles aux axes de coordonnées.
1. Principe de la méthode : Il consiste à faire absorber la dilatation dans une direction donnée par les tronçons perpendiculaires à cette direction. La fraction de la dilatation totale prise en compte par chaque tronçon est donc proportionnelle au cube de leur longueur. Chaque tronçon est supposé se comporter comme une poutre ancrée à ses 2 extrémités ( rotations nulles ).
Soit Dx la dilatation totale à absorber sur ( n ) tronçons L1, L2, ......, Ln . Le tronçon L1 absorbera une fraction de Dx égale à : Ax1 =
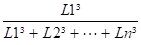
Le dénominateur représentant la somme des longueurs des tronçons élevées au cube, perpendiculaires à l'axe X.
Ainsi, chaque tronçon subira au plus deux déformations suivant deux directions perpendiculaires à son axe.
La tuyauterie sera considérée comme acceptable, sous l'angle de la flexibilité, si chaque tronçon ne subit pas une déformation supérieure à celle qui conduirait à une contrainte de flexion inadmissible. La déformation limite Δlim est donnée par la relation : Δlim =
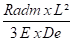
Radm étant la contrainte admissible ( Fig 1-30 ). Il suffira de comparer, pour chaque tronçon, la déformation limite à la déformation résultante réelle. Par exemple, pour un tronçon dirigé vers l'axe Z, il faudra vérifier : Δmax =
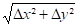
Il est à noter que la société KELLOGG a procédé à une amélioration de cette méthode en incluant un coefficient( f ) permettant d'introduire une rotation limitée due à la flexibilité des tronçons voisins.
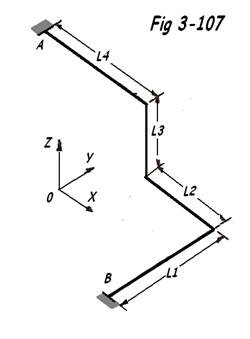
2. Exemple numérique : ( FIG 3-107 )
Données:t° de calcul 320°C ( St 35.8 ---> A106 g A )
dn = 150 ( f 168,3 x 4,5 )
Radm = 82,7 N/mm² ( FIG 1-30 )
a = 4,18 mm/m ( FIG 3-28 )
E = 177.106 Kpa ( à 320°C )
L1 = 8 m ; L2 = 10 m ; L3 = 10 m ; L4 = 15 m
- Tronçons ^ à OX
Dx = ( L4 + L2 ) a = ( 15 + 10 ) x 4,18 = 104,5 mm
DL1 = Dx
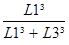
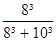
DL3 = Dx
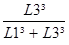
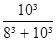
Dy = L1 x a = 8 x 4,18 = 33.44 mm
DL2 = Dy x
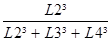
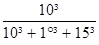
DL3 = Dy x
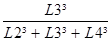
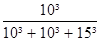
DL4 = Dy x
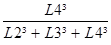
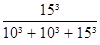
- Tronçon ^ à OZ
Dz = L3 x a = 10 x 4,18 = 41,8 mm
DL1 = Dz x
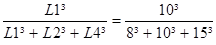
Vérification de la flexibilité
- Tronçon L1 : Dlim =
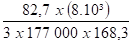
Dmax =
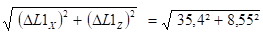
- Tronçon L2
Dlim =
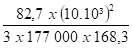
Dmax =
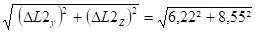
- Tronçon L3
Dlim =
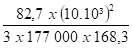
Dmax =
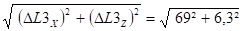
- Tronçon L4
Dlim =
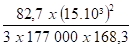
Dmax =
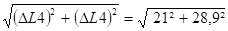
Dernière édition:






