


3.11.5 PROTECTION CONTRE LE GEL
Lorsqu'une tuyauterie véhicule un fluide tel que de l'eau par exemple et que celle-ci est soumise à une température < à 0°C, elle peut subir des dégâts importants dus au gel pour autant que le débit ce réduise ou s'annule. Une isolation aussi épaisse soit-elle ne pourra empêcher ce phénomène, tout au plus pourra-t-elle le retarder, car l'équilibre entre la température du fluide et celle du milieu extérieur finira par s'établir. Deux cas peuvent se présenter, à savoir les cas de la recherche d'un temps ou d'une épaisseur d'isolant et le cas d'une recherche de débit.
1.Cas de la recherche d'un temps ou d'une épaisseur d'isolant
a) Calcul des quantités de chaleur
- Fluide : m1 =
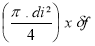
di = diamètre intérieur de la canalisation ( m )
δf = masse volumique du fluide ( kg/m³ )
Qf = cpf . m1 . ( Ti - 273°K )
Ti = température initiale du fluide ( °K )
cpf = chaleur massique à pression constante du fluide J/kg°K
- Tube : m2 = π . di . et . δm = kg/m
et = épaisseur de la tuyauterie ( m )
δm = masse volumique du métal de la tuyauterie ( kg/m³ )
Qm = cpm . m2 . ( Ti - 273°K )
cpm = J/kg°K pour l'acier: cpm = 502 J/kg°K
- Congélation: Qc = Qf . ( 0,25 . m1 )
Qf = chaleur de fusion ( ou de congélation ) du fluide ( Qf = 334 880 J/Kg pour l'eau )
Qc = chaleur nécessaire à la congélation de 25% de la masse de fluide contenu dans un mètre de conduite ( au-delà de cette valeur, les opérations de remise en fonctionnement risquent d'être perturbées ).
b) Déperditions
Q1 =
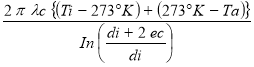
Ta = température de l'ambiance °K
Q2 =
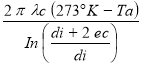
c) Temps pour atteindre l'équilibre des températures
Il est donné par la relation : tE =
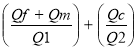
tE =
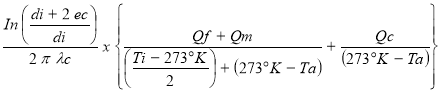
et
ec =
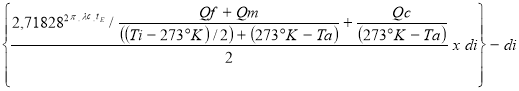
ec = épaisseur du calorifuge en mètre
2. Cas de la recherche d'un débit
Il faut considérer, ici, la déperdition d'énergie par unité de temps pour la longueur totale de la conduite. Nous savons que
Q1 =
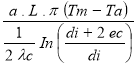
Cette déperdition doit équilibrer l'apport calorifique dû au fluide passant dans la conduite à la température Ti, à celle inférieure à 0°C ( 273°K ) en fonction du débit recherché.
Q1 = Qf . cpf ( Ti - 273°K ) ---> d'où Qm
Exemples numériques
a) Supposons une conduite dn 100 ( ï¦114,3 x 3,6 ) véhiculant de l'eau ayant les caractéristiques
physiques suivantes:
Ti = 281°K ( 8°C ) Chaleur de congélation de l'eau = 334 880 J/kg
δf = 1000 kg/m³ ( soit 80 Kcal/kg dans les anciennes unités )
cpf = 4186 J/kg Température extérieure = - 20°C ( 253 °K )
To = 273°K ( 0°C )
La conduite est munie d'un isolant ayant une conductibilité λc = 0,04 W/m.°K
Quelle sera l'épaisseur ( ec ) de cet isolant nécessaire pour protéger la conduite contre le gel lors d'un arrêt d'une durée de 48 h ( δm ( acier ) = 7850 kg/m³ et cpm = 502,32 J/kg°K )
Solution
m1 =
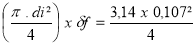
Qf = cpf . m1 . ( Ti - 273°K ) = 4186 x 8,99 x ( 281 - 273 ) = 301 057 J/m
m2 = π . di . et . δ m = 3,14 x 0,1143 x 0,0036 x 7850 = 10,143 kg/m
Qm = epm . m2 . ( Ti - 273°K ) = 502,32 x 10,143 x ( 281 - 273 ) = 40 760 J/m
tR = 48 h x 3600 = 172 800 s
Qc = 334 880 x 0,25 x 8,99 = 752 643 J/m
Notons qu'il n'est pas nécessaire de faire intervenir, ici, Q1 et Q2
ec =
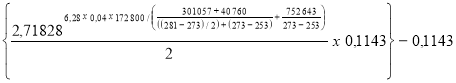
ec = 0,075 m soit 75 mm
Vérifions les valeurs trouvées
Q1 =
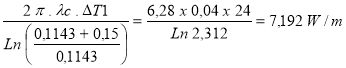
Q2 =
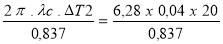
tE =
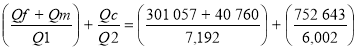
b) Soit une canalisation de longueur L = 20 m en dn 50 ( à˜60,3 x 2,9 ) à la température de -20°C ( température du fluide ) cpe = 4186 J/kg. La température extérieure = - 20°C
Isolant = laine de roche λc = 0,038 W/m°K, épaisseur = 40 mm.
Calculer le débit minimal nécessaire pour éviter le gel dans ces conditions ( To : 0°C = 273°K ).
Solution
Tm =
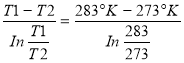
Déperditions horaires en adoptant 20% pour les pertes par supports ( a = 1,2 )
Q1<=
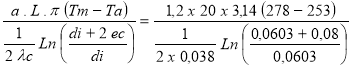
Côté fluide: Q1<= qm . cpe . Δ T = qm x 4186 ( 286 - 273 ) soit qm =
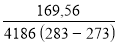
Soit par heure = 0,004 x 3600 = 14,58 kg/h
Soit encore en adoptant un coefficient de sécurité = 1,5, nous obtiendrons 14,58 x 1,5 = 21,874 kg/h ou +/- 22 l/h.
Dernière édition:







