


3.2.2 TUYAUTERIE SOUMISE A PRESSION EXTERIEURE
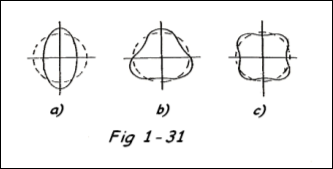
Lorsqu'un tube parfaitement cylindrique est soumis à une pression extérieure (ou au vide intérieur), il est le siège de contraintes identiques mais de signes contraires à celle obtenue pour une mise en pression intérieure. Pour un rapport (e/de) faible (tube mince) le cylindre pourra s'écraser sous l'effet de pe (pression extérieure) ou du vide intérieur c'est en fait un phénomène semblable à celui de flambage d'une poutre chargée à son extrémité suivant son axe. C'est un phénomène brutal.
Pratiquement, on estime qu'une tuyauterie soumise au vide intérieur (ou à une pression extérieure de +/- 1 barg) résistera si le rapport e/de = 0,011, c'est-à -dire que l'épaisseur du tube serait de l'ordre du 1/100 du diamètre extérieur ( e étant l'épaisseur hors tolérance et surépaisseur de corrosion )
Des études ont montré que e /de =
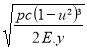
pc = pression critique (N/mm²)
Ey = module de Young (ou d'élasticité) (N/mm²)
μ = coefficient de Poisson (μ = 0,3 pour l'acier)
Ainsi, pour un tube en acier, la ruine est donnée par la relation
pc =
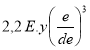
3.2.2.1 Détermination de l'épaisseur d'un tube droit soumis à pression extérieure (ou au vide intérieur) st code ASME VIII div 1 paragraphes UG-28 à UG-30.
Paramètres de calculs
de = diamètre extérieur de tube (mm)
e = épaisseur minimum du tube (surépaisseurs et tolérances déduites)
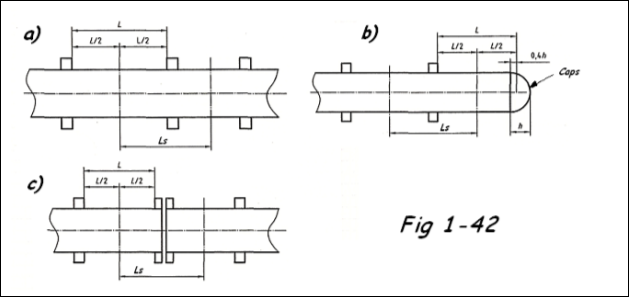
L = pour de et L constants, c'est la plus grande distance entre 2 points de renforcement reconnus par l'ASME.
- jonction d'un cylindre et d'un cône (réduction)
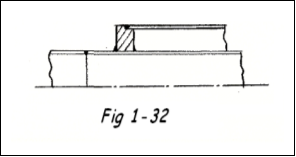
- un anneau renfort (extrémités d'une tuyauterie : double enveloppe (JACKETED PIPE) pour le réchauffage des fluides par exemple
- Un CAPS (fond bombé) à 1/3 de la hauteur à partir de la fonction avec le tube.
- Prendre une valeur de e et calculer les rapports de/e et L/de
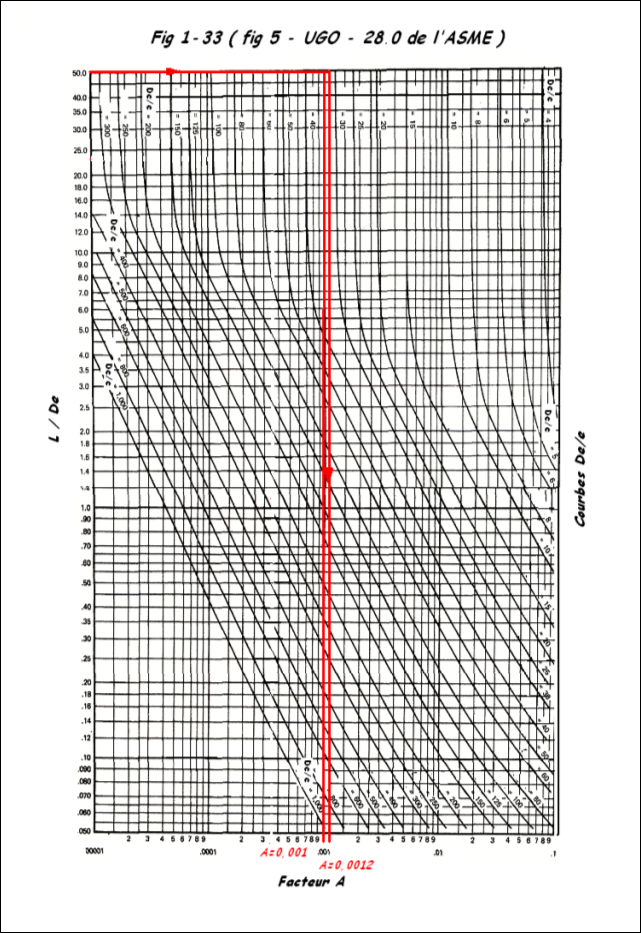
- Prendre la fig 1-33 (5-UG0-28.0 code ASME VIII) et placer en ordonnée la valeur de L/de. Pour des valeurs L/de inférieure à 0,05 se placer en ordonnée à la valeur 0,05. Partant de l'ordonnée tracer une horizontale jusqu'au point d'intersection avec la courbe à la valeur de de/e précédemment calculée (interpolation autorisée). Par ce point d'intersection, tracer une verticale donnant ainsi la valeur de A.
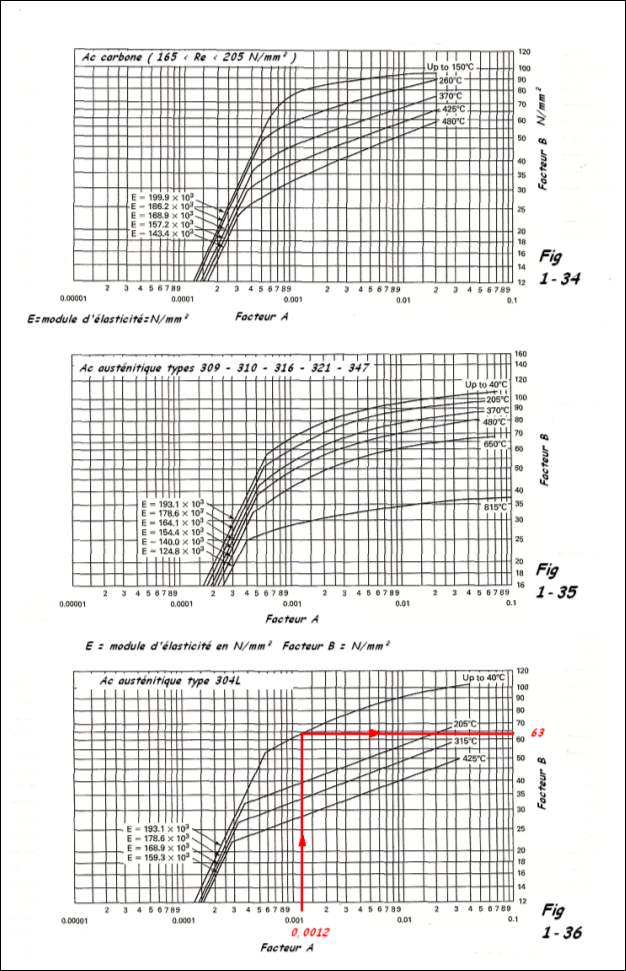
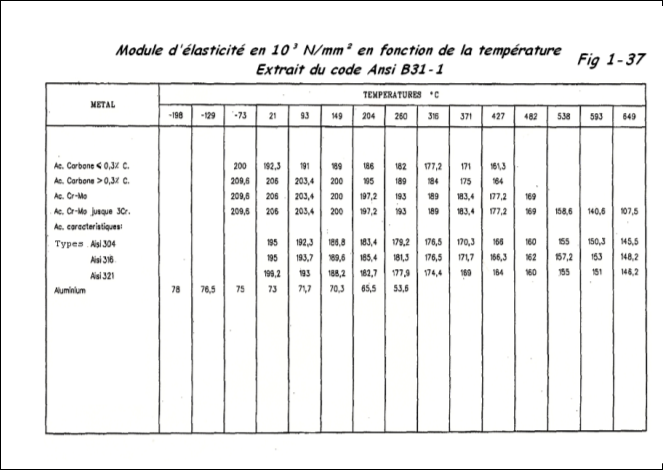
- Avec cette valeur de A, entrer le graphique fonction du matériau choisi (fig 1-34 = acier carbone ou faiblement allié; fig 1-35 = aciers austéristiques Aisi 316, 321, 347, fig 1-36 = acier Aisi 304L) pour les autres types de matériaux, consulter l'annexe 5 de code ASME VIII div 1. Tracer en A une verticale jusqu'au point de rencontre avec la courbe de température (interpolation permise entre 2 courbes). Par ce point, tracer une horizontale donnant la valeur de B en psi (rappel 1000 psi = 1ksi = 6.9 N/mm²).
- Si A tombe à gauche de la ligne de température, la pression extérieure autorisée est déterminée par la relation :
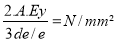
Ey = module de Young du matériau (N/mm²) à la température de calcul (Fig 1-37)
- Dans tous les autres cas, on calcule la pression extérieure sur base de la valeur de B convertie en N/mm² (MPa), selon la relation
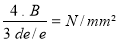
Si pe >= à la pression extérieure de calcul, l'épaisseur du tube est suffisante. Dans le cas contraire, augmenter l'épaisseur et recommencer les calculs.
2. Tubes pour lesquels de/e < 10
- Déterminer la valeur du facteur B, de la même manière que précédemment. Lorsque de/e < 4, calculer A à l'aide de la formule :A =
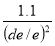
- A l'aide du facteur B déterminé précédemment et converti en N/mm², calculer une valeur pe1 (N/mm²) à l'aide de la formule
Pe1 =
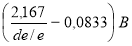
Calculer également une valeur pe2 telle que :
Pe2 =
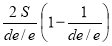
S étant la plus petite des 2 valeurs suivantes
- 2 x tension admissible à la température de calcul de la matière (fig 1-30)
- 0.9 x Ret (limite élastique à la température de calcul)
S =
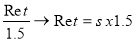
La valeur de S est donnée à la Fig. 1-30
ex : acier A106g.B t° : 316°C S = 103,4 N/mm²
Soit Ret = 103,4 x 1,5 = 155,1 N/mm².
La pression extérieure maximale (pe) sera la plus petite des valeurs de pe1 et pe2 calculée ci-avant.
Si cette valeur pe >= p extérieure de calcul, l'épaisseur du tube choisi est suffisante. Dans le cas contraire, augmenter l'épaisseur et recommencer le calcul.
3. Calcul des anneaux raidisseurs
a) Paramètres de calcul (ASME VIII paragraphe UG 29)
AS = Section de l'anneau raidisseur (mm²)
LS = La moitié de la distance parallèle à l'axe du tube, de la ligne de symétrie de l'anneau raidisseur, jusqu'au point de renforcement suivant l'un des côtés plus la moitié d'une distance similaire à l'autre côté (mm)
L = Voir ci-dessus (mm)
pe = pression extérieure de calcul (N/mm²)
de, e = (voir ci-dessus) mm
I = moment d'inertie de l'anneau raidisseur autour de son axe entre // à l'axe du corps (mm4)
I' = moment d'inertie autour de son axe neutre parallèle à l'axe du tube, de la combinaison de la section, de l'anneau raidisseur et une partie du corps, d'une longueur totale =
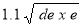
b) Dimensionnement de l'anneau raidisseur
Choisir un profilé. Calculer As et B
B =
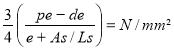
Convertir B en psi (1N/mm² = 144,927 psi)
- Sur le graphique correspondant au matériau choisi (fig 1-34 à 1-36) entrer la valeur de B jusqu'à l'intersection avec la courbe de la température de calcul (interpolation permise). Par ce point, tracer une verticale qui donnera la valeur de A en abscisse. Lorsque le corps de l'anneau raidisseur est constitué de matières différentes, utiliser le graphique du matériau donnant pour A, la valeur la plus élevée. Si, sur le graphique B tombe sous l'extrémité gauche de la ligne de température, on peut calculer A à l'aide de la formule :
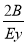
Dans le cas des tubes, on considère uniquement l'anneau
raidisseur soit :
Is =
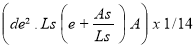
Pour rappel, I pour une section rectangulaire est donnée par la relation :
I =
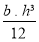
Si I < Is, il faut choisir un anneau raidisseur plus important
et recommencer le calcul.
4 . Exemples de calcul
a) Soit un tube  60,3 x 2 cm en inox Aisi 304L soumis au vide (soit pe ï‚» 1barg) sous une t° de 20°C.
Sa longueur entre 2 points de renforcement est de 30m. Peut-il résister au vide d'après l'ASME VIII ?
épaisseur de calcul = 2/1,125 = 1,77 mm ( hors tolérance et surépaisseur de corrosion ).
Rapport de/e = 60,3 / 1,77 = 34,1 > 10 (tube mince)
L/de
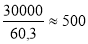
D'après l'ASME VIII UG 28, pour des valeurs de L/de > 50 se placer en ordonnée sur 50 (Fig. 1-33) via la courbe de/e = 34,1 nous obtenons A = 0,0012
Prenons le graphique Fig 1-36 : t = 20°C inférieur à 40°C avec A = 0,0012, nous obtenons B = 63 N/mm².
(A) tombe à droite de la courbe de température soit :
pe =
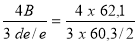
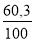
Remarque : Attention au supportage de la conduite qui devra être conforme au tableau Fig 3-34 soit 4,3 m max entre supports afin que la flèche reste inférieure à L/1000, ce qui limite la contrainte de flexion ( compression dans les fibres supérieures ).
b) Soit un tube à double enveloppe ( Fig 1-39 ) . La tuyauterie intérieure ( dn 150 sch 10s ) en ac. Inox
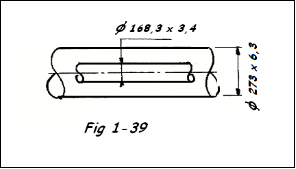
Solution
Les brides d'extrémité sont admises comme renforcement
La portée proposée est trop importante pour notre tube dn 150 sch 10s. Le tableau Fig 3-34 de la Partie 3 nous indique que pour une flèche L/1000 la portée ne peut dépasser 8,69 m. Nous diviserons donc la distance entre brides par 2 et nous placerons un anneau renfort, soit Ls = 6 m épaisseur nette
tube dn 150 = 3,4 x 0,125 ï‚» 0,4mm, soit une épaisseur nette de 3,4 - 0,4 = 3mm.
de/e =
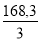
L/de =
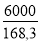
Ey = 186,5 kPa à 150°C soit 186500 N/mm²
Le graphique Fig 1-33 donne A = 0,0001.
Sur le graphique Fig 1-40 pour l'ac. Inox AISI 304, portons la valeur de A jusque la courbe de température t = 150°C et nous obtenons le facteur B ≈ 52,5 N/mm². Nous devons utiliser l'équation
pe =
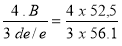
Nous adopterons, en première approximation, un anneau renfort de section 10 x 20 afin qu'ils puissent glisser dans le tube supérieur et que la section de passage entre gaine dn 250 et l'extérieur de l'anneau laisse passe la vapeur et les condensats. Notons qu'il faut souder ( par exemple ) deux bouts de tubes dn 15 ou dn 20 en inox, placés à 30° de part et d'autre de l'axe vertical soudés sur l'anneau, pour faire reposer le tube intérieur et laisser passer les condensats.
Note : Si ce montage n'est pas réalisable, il faut prévoir un tube by-pass avec soupape et purgeur.
As = 10 x 20 = 200mm², pe = 0.5 N/mm²
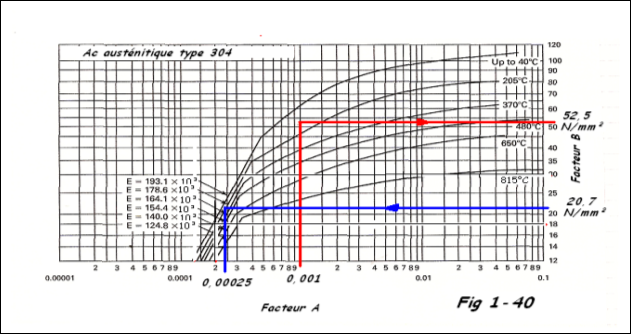
B =
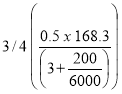
Reprenons le graphique Fig 1-40 portons B = 20,8 N/mm² jusqu'à la courbe de température t = 150°C et Ey = 186,5 . 10³ N/mm² nous obtenons A ≈ 0.00025.
Is =
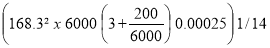
Moment d'inertie du renfort I =
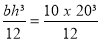
Is =
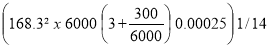
I =
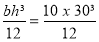
I > Is l'anneau renfort est suffisant.
3.2.2.2 Détermination de l'épaisseur d'un tube droit soumis à pression extérieure suivant le code EN 13480-3 édition 2002 art. 9
1. Paramètres de calculs ( hors du domaine de fluage )
Voir le § 3.2.2.1, toutefois :
La pression extérieure à prendre en compte est la pression max, si la pression intérieure ne peut descendre sous la pression atmosphérique. Si la pression intérieure peut descendre sous patm :
La pression extérieure sera 1 barg si la tuyauterie n'est soumise qu'à la pression atmosphérique ou sera égale à la pression entre les deux enveloppes + 1 barg .
Les règles de l'article 9 ne sont valables que si la non-circularité est ≤ 0,5% du rayon de la conduite.
N.B : Les calculs de vérification ne sont pas nécessaires pour les tuyauteries en ac-c ou acier faiblement allié pour t ≤ 150 °C et en acier austénitique pout t ≤ 50 °C et soumises à une pression extérieure ≤ 1 barg si e/de ≥ 0,01 et une non-circularité ≤ 1% et plat local < e.
Limites de contraintes dans le domaine élastique
Acier au carbone ou faiblement allié : S = Ret(0,2%) pour les tubes et les renforts
Aciers austénitiques : S = Ret(0,2%) / 1,25 pour les tubes et renforts.
Les longueurs L et Lc seront déterminées à partir des Fig 1-42 a, b , c
- Effondrement entre les raidisseurs
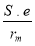
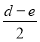
Déterminer pm =
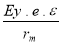
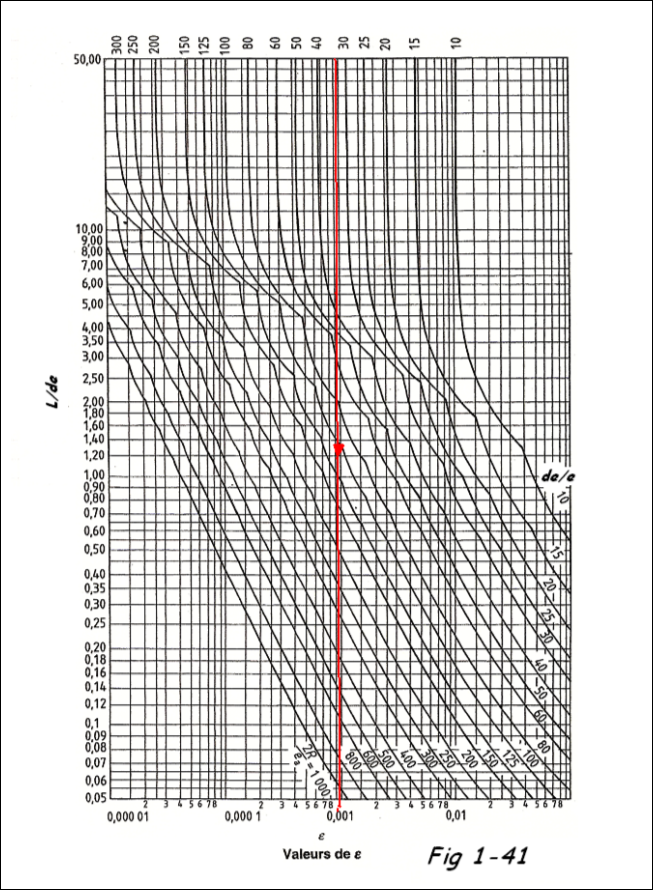
La norme donne une formule itérative très longue pour calculer le facteur ε , mais bien qu'elle ne le précise pas, on pourrait utiliser l'abaque ( Fig 1-41 ) de la EN 13445-3 ( chaudronnerie ), comme on le fait pour l'ASME => ( ε ≈ A ).
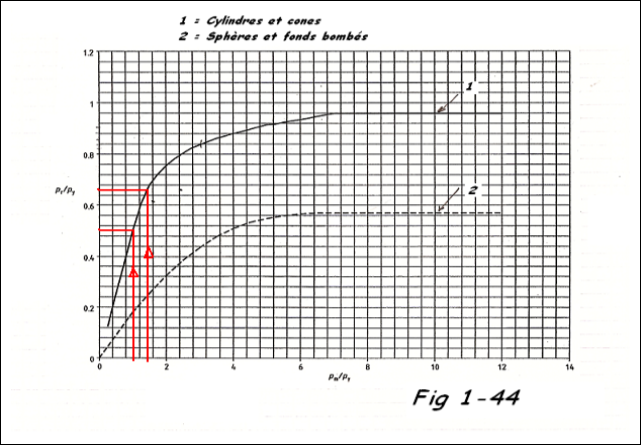
Ensuite, calculer le rapport pm /py et à partir des courbes Fig 1- 44 déterminer le rapport pr/py
Pr doit alors satisfaire à la relation pr ≥ k . p avec k = 1,5 sauf pour les aciers moulés ou k = 1,875.
Si pr < k . p il faut augmenter la valeur de e ou diminuer l'espace entre les raidisseurs L ou Ls .
b) Effondrement global des tuyaux comportant des raidisseurs
Calculer pn =
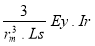
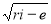
pn ≥ k . ks . p ( ks = 1,33 pour les raidisseurs formés à froid ), dans le cas contraire, il faut un renforcement plus important ou supplémentaire ou encore augmenter la valeur de ( e ) .
Calculer pys =
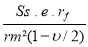
Calculer pn ( pression d'instabilité élastique d'un cylindre avec raidisseur ) pn =
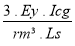
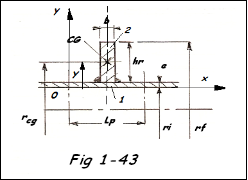
Icg =moment d'inertie de la section droite comprenant raidisseur + section participante de longueur
Lp =mm4 ( voir Fig 1-43 ). Puis calculer σs ( contrainte max dans un raidisseur )
σs =
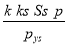
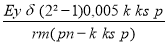
Dans laquelle
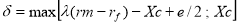
de la EN 13480-3 mais qui n'est pas cohérente au niveau unitaire ( mm³ + mm ? ). En nous reportant à la formule similaire de la EN 13445-3, relative aux cylindres soumis à pression extérieure nous pensons que
La formule ci-après est plus réaliste ( sous réserve ). Xc =
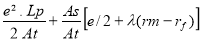
Avec At = As + ( e . Lp ) et λ = 1 pour les raidisseurs intérieurs ou -1 pour les raidisseurs extérieurs.
Il suffit de vérifier que 0 ≤ σs ≤ Ss . Si cette condition n'est pas satisfaite, il faut procéder à un renforcement supplémentaire ou plus important, ou augmenter l'épaisseur du tube intérieur.
Dans tous les autres cas de renforcement, le lecteur se reportera à la norme EN 13480 dernière édition.
Remarque : - Les réductions peuvent, sous certaines conditions, être considérées comme étant un raidisseur effectif ( voir art. 4 de l' EN )
- Les fonds bombés ( caps ) seront vérifiés en tenant compte de la procédure suivante,
pour autant que l'imperfection du rayon soit ≤ 1% et que le rayon de courbure basé sur une longueur
d'arc = 2,4
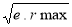
- Choisir une valeur pour ( e ) et calculer py =
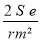
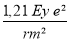
- A partir des courbes Fig 1-44 déterminer pr/py à partir de pm / py et déterminer pr qui doit satisfaire à pr ≥ k . p ( voir tubes droits ). Si pr < k . p il ya lieu d'augmenter la valeur de e.
3. Exemples numériques
Nous allons reprendre les applications numériques traitées avec l'ASME et nous réaliserons les calculs sur base de l'EN 13480-3
a) Données : tube Ф 60,3 x 2 mm en Aisi 304 L ( 1.4301 ) soumis au vide extérieur p ≈ 1 barg sous t = 20°C . La longueur entre 2 renforcements admis ( brides ) L = 30m. Epaisseur de calcul e = 1,77 mm.
Solution
Rapports : de/e =
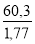
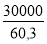
De même que pour l'ASME, pour les valeurs de L/de > 50 se placer en ordonnée sur 50 ( Fig 1-41 )
et nous obtenons, ici aussi, ε ≈ 0,001.
py =
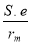
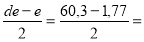
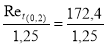
py =
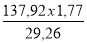
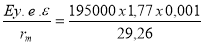
pm / py =
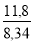
pr = 8,34 x 0,5 = 4,17 N/mm² et pr ≥ k . p = 1,5 x 0,1 = 0,15 N/mm² . Donc 4,17 > à 0,15 l'épaisseur du tube est suffisante.
b) Données : tube intérieur Ф = 168,3 x 3,4 mm en Aisi 304 soumis à la pression extérieur de 5 barg et pi = 0 barg ( = patm ). La longueur entre anneau renfort Ls = 6 m ( voir calcul suivant l'ASME ), épaisseur de calcul = 3 mm.
Solution
Rapports : de/e =
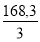
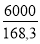
Le graphique Fig 1-41 donne ε ≈ 0,001 . Ss =
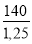
rm =
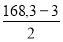
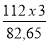
pm =
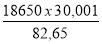
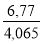
La Fig 1-44 courbe 1 nous donne pr / py ≈ 0,7 => soit pr = 4,065 x 0,7 = 2,85 N/mm²
pr ≥ k . p = 1,5 x 0,5 = 0,75 N/mm² => 2,85 > 0,75 N/mm² le tube résistera sur toute sa longueur.
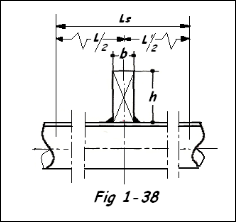
Reprenons les dimensions de l'anneau renfort adopté lors du calcul selon l'ASME, soit b = 10 mm et h = 30 mm. Nous devons calculer le moment d'inertie ICG comprenant la section e l'anneau et section du tube de longueur Lp = 1,56

Calculons la position du CG de l'ensemble S1 et S2 par rapport à 0X
S1 = 3 x 24,34 d1 = 1,5 Mt = 1 09,53 mm³
S2 = 10 x 30 d2 = 18 = 5400 "
--------- ----------
∑= 373,02 mm² = 5509,5 mm³ y =
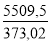
soit ICG = ∑
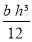
Pour le calcul de Xc voir notes ci-avant. Xc =
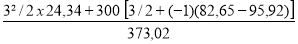
δ = max
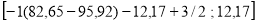
pys =
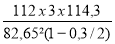
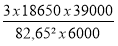
σs =
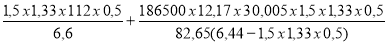
σs < Ss , le renforcement est accepté.
Dernière édition:






