


2.11.3 CALCULS RDM DES SUPPORTAGES
1. Calcul des "Trunnions" (attaches intégrales)
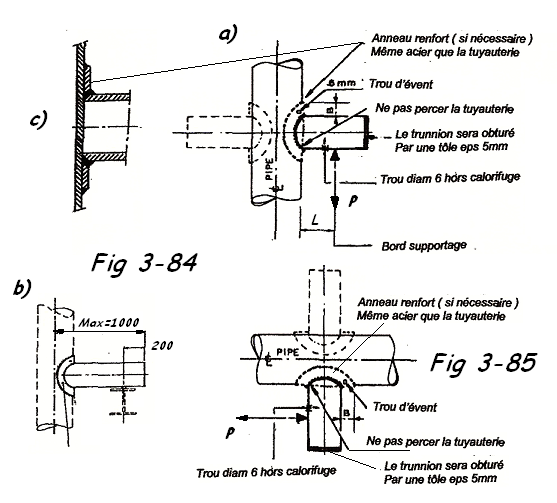
Les trunnions ou tourillons sont très utilisés sur les tuyauteries à haute température. Ils sont constitués par un bout de tube soudé sur la tuyauterie, de même qualité que celle-ci. Si cette tuyauterie est verticale (Fig. 3-84) ils sont appelés "Supports", ou horizontale, il sont sont appelés "Tirants".
L'extrémité des trunnions sera fermée par une tôle percée d'un petit trou ou le trunnion sera bourré de calorifuge.
On doit vérifier que la contrainte due au moment de flexion σf = P.L /
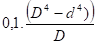
et au cisaillement (tc = P/2 . p. rm . et) soit au total si =
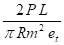
P = effort (réaction sur le trunnion) (N)
L = distance du point de pose (ou d'accrochage) par rapport à la génératrice extérieure du tube (mm)
Rm = rayon moyen de trunnion (mm) et =épaisseur du trunnion (mm)
Radm = contrainte nominale de calcul à la t° de calcul en fonction de la nuance du matériau (Fig. 1-30);
0,8 prend en compte la résistance de la soudure.
2. Calcul d'un point fixe sur une colonne (exemple)
Soit un point fixe représenté à FIG 3-97 et placé sur une colonne d'un bâtiment. Cette colonne étant supposée parfaitement stabilisée. Le calcul de la tuyauterie a donné les efforts suivants:
Fx = 800 daN Mx = 450 mdaN
Fy = 600 daN My = 650 mdaN
Fz = 800 daN Mz = 450 mdaN
Problème : vérifier la résistance de ce point fixe:
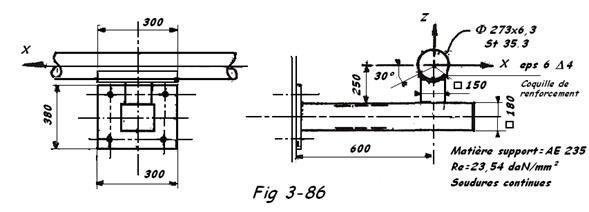
a) Vérification de la coquille de renforcement ( soudure a = 4 mm périphérique et continue )
Soit 2 cordons latéraux Ll = 2 x 300 = 600 mm
2 cordons frontaux Lf = 2
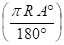
Lf = 2
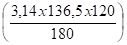
Les cordons de 4 mm conviennent puisque a < 0,7 x e soit 0,7 x 6 = 4,2 mm
Contraintes dans l'ensemble des cordons
Cordons frontaux :
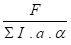
pour a à˜4 mm a = 1
Cordons latéraux :
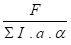
pour a à˜4 mm a = 1
On peut simplifier les calculs en donnant une formule enveloppe identique pour les cordons latéraux et frontaux soit :
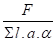
α = 1 pour a ≤ 4 mm et α = 0,8
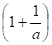
R'adm =0,75 x 15,8 daN/mm² = 11,85 daN/mm² ( attention tenir compte du § 2.5.3 pour supports soumis à température ).
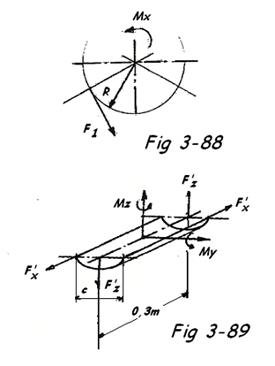
- Calcul de l'effort F1 provoqué par Mx = 450 mdaN avec R = 0,1365 m
Soit F1 =
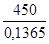
My donne lieu à un couple comme le montre la Fig 3-89 =>
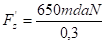
Mz donne également lieu à un couple : c = corde = 2 R sin β /2 = 2 x 137,5 x sin 120° /2 =238 mm
Soit c = 0,238 m et Fx' =
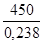
Soit FT = Fx + Fy + Fz + F1 + ( F'x x 2 ) + ( F'z x 2 )
FT = 800 + 500 + 800 + 3297 + ( 1891 x 2 ) + ( 2167 x 2 ) = 13513 daN
Longueur totale des cordons = ( 2 x 600 ) + ( 2 x 571,5 ) = 2343 mm
s =
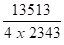
b) Vérification du caisson de liaison coquille - console
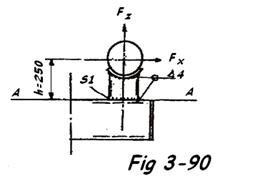
La Fig 3-90 montre que c'est la soudure S1 qui est la plus sollicitée ou le caisson lui-même.
Efforts sur la ligne des soudures A-A
Fx = 800 daN
Fy = 500 daN
Fz = 800 daN
MxAA = Mxo + Fyo x h
MyAA = Myo + Fxo x h
MzAA = Mzo
Vérifions le profilé 180 eps 8
Caractéristiques mécaniques tirées du catalogue CBLIA
Ixx = 2591 cm4 I/vx = 288 cm3
Iyy = 2591 " I/vy = 288 "
Note : Lorsqu'il existe, comme c'est le cas ici, des moments de torsion assez important il est recommandé de ne pas utiliser des profilés I, U, L qui sont instables à la torsion.
184 - 16,44
Io/v = ----------------- = 427,4 cm3
3 x 18 x à– 2
1265
sfx = ---------- = 4,4 daN/mm²
288
930 sf = 4,4 + 3,25 = 7,65 daN/mm²
sfz = ----------- = 3,25 daN/mm²
288
1130
t= --------- = 2,65 daN/mm²
427,4
si =
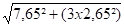
Vérifions les soudures de la FIG 3.91
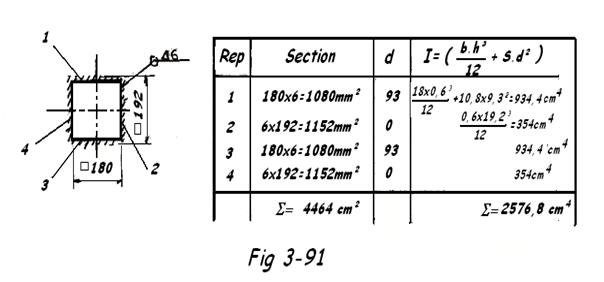
Ixx = Iyy = 2576,8 cm4
I/vx =
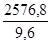
S = 4464 mm²
Section à l'effort tranchant suivant X ou suivant y = í(180 + 12 ) x 6 འx 2 = 2304 mm²
Io/v soudure =
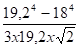
Calcul des contraintes:
FxE = 800 daN tcis =
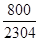
FyE = 500 daN st =
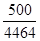
FzE = 800 daN tcis =
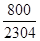
MxE = 1265 mdaN sf =
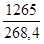
MyE = 930 mdaN tt =
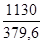
MzE = 930 mdaN sf =
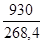
stotal = 0,12 + 4,7 + 3,5 = 8,32 daN/mm²
ttotal = 0,34 + 0,34 + 3 = 3,68 daN/mm²
si =
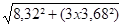
Contrainte admissible dans la soudure à 6 : a= 0,8
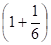
R'adm = 0,75 x 0,933 x 15,7 = 11 daN/mm² > 10,5
d) Calcul de la platine et des boulons de fixation
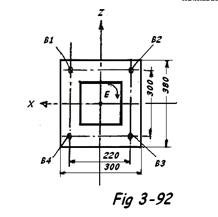
La platine est destinée à être fixée sur une colonne d'un bâtiment ( IHE 300B ), au droit d'un plancher pour une bonne résistance à la torsion et ce au moyen de boulons M24 HR ( 8.8 ). Nous avons en ( c) ) déterminé les efforts et moments en E. Il y a maintenant lieu de rechercher les efforts maxima our le calcul des boulons.
- Efforts de traction
B1 B2 B3 B4
FyE = 500 daN =>
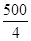
MxE = 1265 mdaN =>
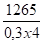
MzE = 930 mdaN =>
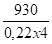
Efforts max ( traction ) dans le boulons B2 = 125 +1054 + 1057 = 2236 daN
- Efforts de cisaillement
B1 B2 B3 B4
FxE = 800 daN soit =
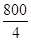
FzE = 800 daN soit =
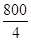
MyE = 1130 mdaN soit =
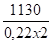
Effort max ( cisaillement ) dans les boulons = 200 + 200 + 2568 = 2968 daN
Vérification du boulon B2 supportant un effort de traction = 2236 daN et un effort de cisaillement de 2968 daN.
Section résistante d'un boulon M24 (8.8 ) = 353 mm² suivant tableau FIG 3-93
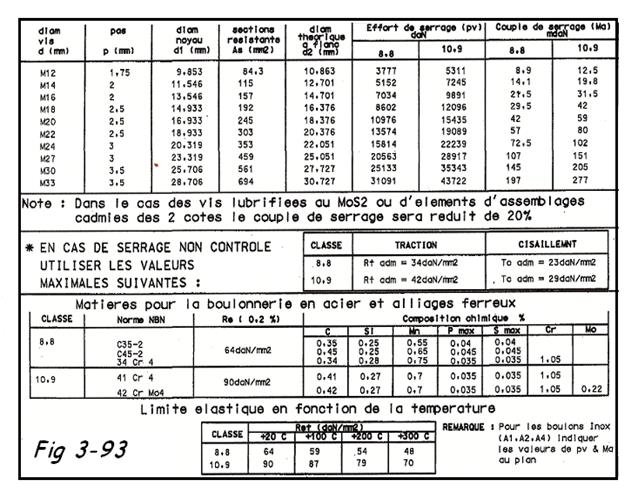
s=
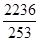
t=
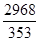
si =
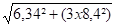
Vérification de la platine de fixation
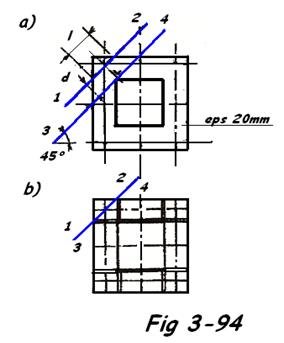
Section de calcul = section 1-2 (à relever à l'échelle)
Soit d = 50 mm et l = 110 mm épaisseur platine = 20 mm
Effort de traction = 2236 daN
Mf = 2236 x 0,05 m = 112 mdaN
σ =
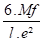
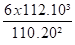
( Pour autant que le support ne soit pas soumis à température ).
Remarque : Dans le cas de fortes sollicitations, il faudra prévoir des goussets ( Fig 3-94b ) afin de réduire les distances d et par là le moment donc la contrainte.
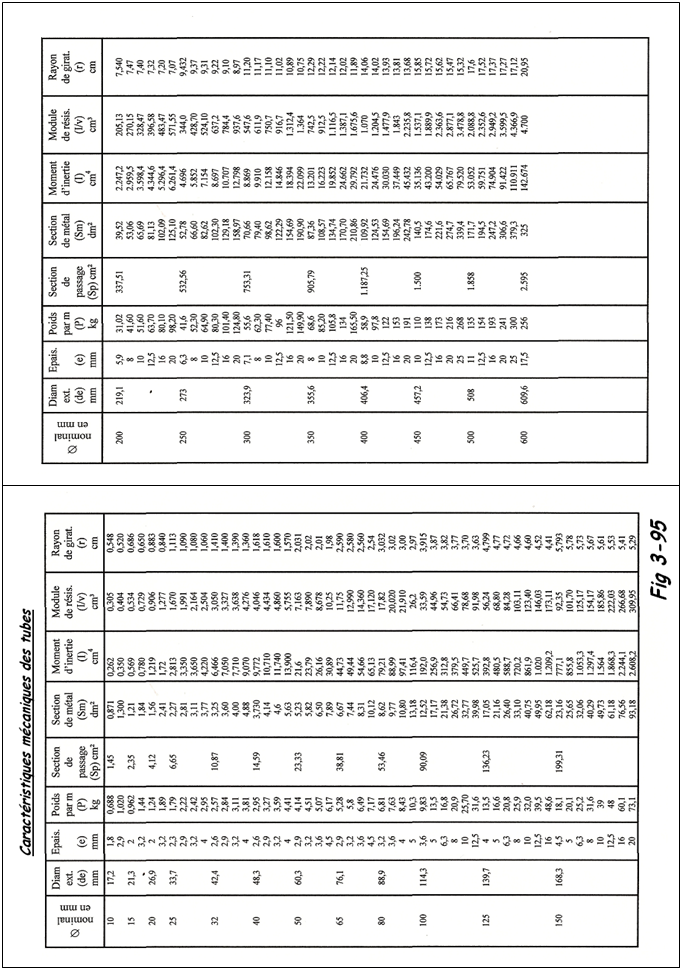
Dernière édition:






