2.11 METHODES SIMPLIFIEES POUR DETERMINER UN SUPPORTAGE
2.11.1 CALCUL DES FLECHES DANS LES TUYAUTERIES
Il existe, dans de nombreux catalogues ou ouvrages techniques, des abaques permettant de déterminer avec une bonne approximation, la pente et la flèche maximales des tuyauteries véhiculant des gaz ou des liquides. Toutefois, les calculettes électroniques actuelles sont très performantes et souvent programmables, permettant de calculer rapidement et facilement ces renseignements, à partir des relations ci-dessous par exemple, en sachant que la charge ( uniformément répartie ) exprimée en daN/m comprend le poids du tube + le poids du fluide + le poids du calorifugeage éventuel.
1. Tuyauteries posées sur deux appuis
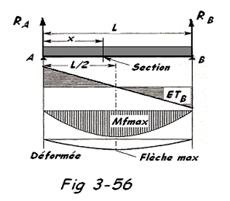
RA = RB =
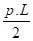
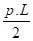
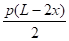
Mx = px
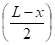
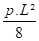
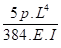
2. Tuyauteries posées sur trois appuis
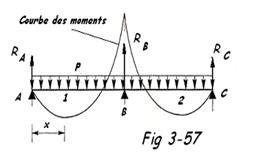
RA = RC =
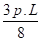
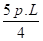
MB = -
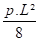
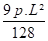
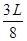
M = 0 à
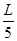
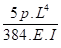
f1 = f2 = 0,415 fo
3. Tuyauteries posées sur 4 appuis
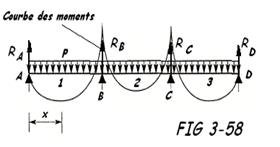
RA = RD =0,40 p . L ; RB = RC = 1,10 p . L
MB = MC = -
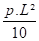
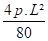
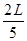
M = 0 à
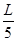
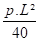
M = 0 à 0,28 L de l'appui B et C
fo = -
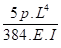
Note : On se limite toujours à 4 appuis maximum, vu que les flèches ne varient pratiquement plus avec la multiplication des appuis. Par sécurité et surtout pour les conduites contenant des liquides dangereux ou de la vapeur saturée, on utilise généralement le cas des tuyauteries posées sur deux appuis.
4. Exemple numérique
Supposons une tuyauteries en ac. St 35.8 de Ф 168,3 x 4,5 remplie d'eau ( δ = 1000 kg/m³ ) et calorifugée dont le poids est de 8,05 daN/m. Calculer la réaction aux appuis A et B, le moment fléchissant max ainsi que la flèche maximale pour x = L/2, sachant que la portée max est de 7 m et que la température de service = 150°C.
Solution
Tube Ф 168,3 x 4,5 = 18,1 daN/m
Eau dans le tube = 20 daN/m
Calorifuge = 8,05 daN/m
P(total) = 18,1 + 20 + 8,05 = 46,15 daN/m
RA = RB =
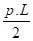
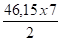
Mmax = -
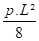
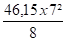
I ( tube ) = 777,1 cm4 et I/V = 92,35 cm³ soit σ =
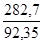
Voir tableaux précédents.
fo = -
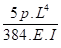
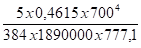
soit 1/712 de la portée, c'est une valeur un peu importante mais acceptable dans ce cas, rappelons que le tableau Fig 3-31 donnait pour ce cas précis L = 6,6 m.
Si le même tube était posé sur 4 appuis, nous aurions : f1 = 0,519 fo = - 0,51 cm ( 1/1372 de la portée )
f2 = 0,039 fo = - 0,0383 cm ( 1/18276 de la portée ).
2.11.2 METHODE APPROCHEE POUR LE CALCUL DES CHARGES ET DEPLACEMENTS DU SUPPORTAGE
1. Rappel de statique
Il est évident que les calculs qui suivront peuvent être directement réalisés en utilisant un logiciel de calcul de tuyauteries ( ex. PIPEPLUS de ALGOR ), mais il est parfois plus rapide de calculer les efforts en utilisant les principes de la statique ( rappel: voir COURS DE MECANIQUE GENERALE ). Ce calcul est basé sur l'équilibre des poutres chargées reposant sur 2 appuis, Les réactions en A et B sont déterminées par les 3 équations d'équilibre ( 2 équations de projection et 1 équation des moments ).
∑alg ProjV F = 0
∑alg ProjH F = 0
∑alg MA F = 0
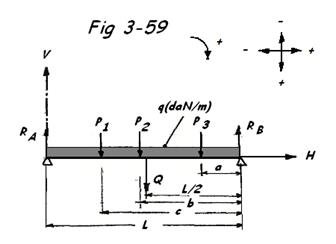
Dans le cas de la Fig 3-59, nous n'aurons que deux équations d'équilibre à satisfaire :
- RA + P1 + P2 + P3+ Q - RB = 0
RA + RB = P1 + P2 + P3 + Q
RA =
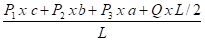
Q = q x L = daN
q = poids de la tuyauterie avec fluide de circulation + calorifuge ( daN/m )
Dans le cas de 2 travées voisines, la réaction sur l'appui commun sera égale à la somme des réactions de chacune des 2 travées sur cet appui.
2 Méthode approchée
Cette méthode est basée sur l'hypothèse que le déplacement thermique d'un point courant d'une branche est proportionnel à la coordonnée du point par rapport à son point fixe.
Mise en oevre de la méthode
- Réaliser un isométrique de la conduite
- Localiser les divers points de supportage
- Calculer la répartition des charges de la tuyauterie
- Calculer les charges individuelles des supports ( la tuyauterie étant considérée comme une poutre RDM )
- Calculer la dilatation thermique de la tuyauterie
- Calculer le déplacement des supports dû au déplacement de la tuyauterie dans son ensemble.
- Calculer le déplacement résultant des supports.
- Choisir le modèle et le type de support.
a) Détermination des déplacements thermiques des branches verticales et horizontales
1 Déplacements des branches verticales
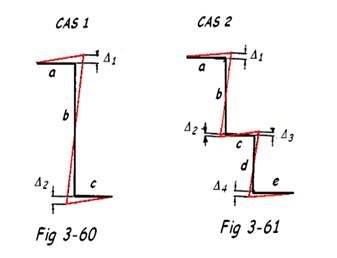
Cas 1 : Fig 3-60
Δ1 + Δ2 = Δb
Δ1 =
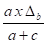
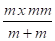
Δ2 = Δb - Δ1
Cas 2 : Fig 3-61
Δ1 + Δ2 = Δb Δ3 + Δ4 = Δd
Δ1 =
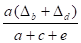
Δ2 = Δb - Δ1
Δ1 =
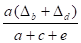
Δ3 = Δd - Δ4
Cas 3 : Fig 3-62
Δ1 + Δ2 = Δb ; Δ3 + Δ4 = Δd ; Δ5 + Δ6 = Δf
Δ1 =
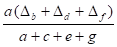
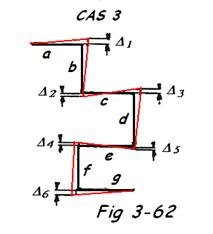
Δ3 =
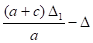
Δ6 =
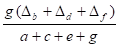
2. Répartition des déplacements
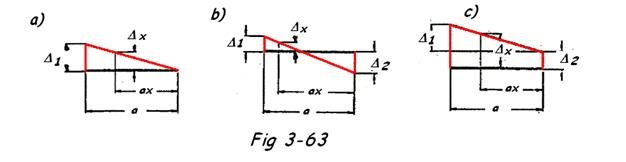
Fig 3-63a : Δxx=
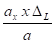
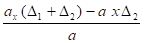
Fig 3-63c : Δx =
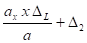
b) Solutions par approximations pour le dimensionnement des suspensions à ressort
1. Détermination du type de ressort
Charge, course du ressort, encombrement et fixation du ressort, sont déterminés par les caractéristiques de la tuyauterie. La majorité des cas rencontrés dans la pratique réclament la possibilité de déplacements horizontaux et verticaux. Le support représenté Fig 3-64, doit avoir une course de ressol = ΔL et permettre un déplacement angulaire ≤ 4°. La distance entre les supports est imposées par les tableaux Fig 3-31 ou suivants.
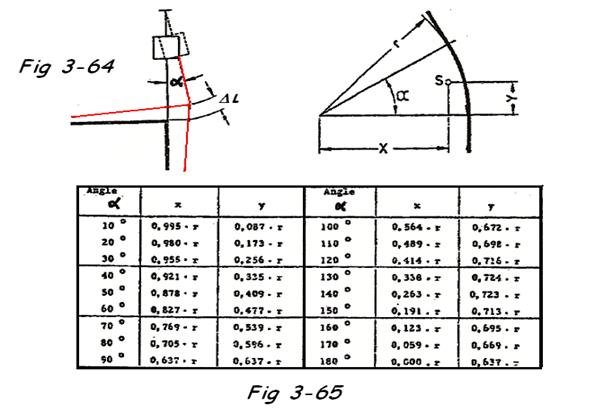
c) Recherche du centre de gravité ( CG ) d'une courbe Fig 3-65
X =
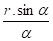
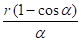
3. Exemple de calcul
a) Données du problème
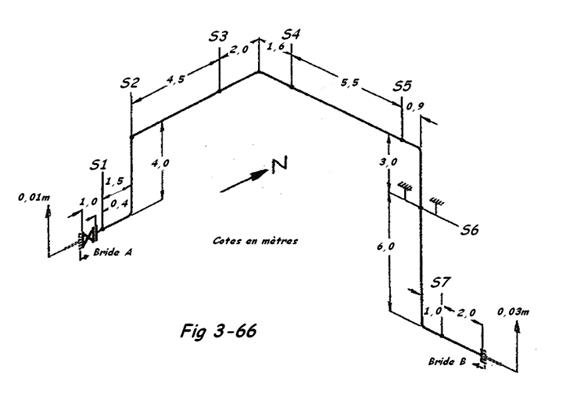
Tuyauterie dn 150 ( Ф 168,3 x 4,5 ) en acier St 35.8 selon iso Fig 3-66.
Température de calcul = 380°C ( soit 365 + °C => pour rappel voir 1ère partie )
Pression de calcul = 11 barg ( pression de service + 1 bar ou + 10% selon le cas => voir 1ère partie )
Vanne dn 150 Pn 16 à brides : poids = 82,4 daN/m + 8,05 daN/m de calorifuge.
Brides dn 150 Pn 16Din 2633 en C22N : poids = 7,7 daN/bride.
Dilatation à 380°C selon le tableau Fig 3.28 par interpolation.
b) Position du support S6
Soit la Fig 3-67 reprenant la branche de droite, entre le support S5 et la bride B.
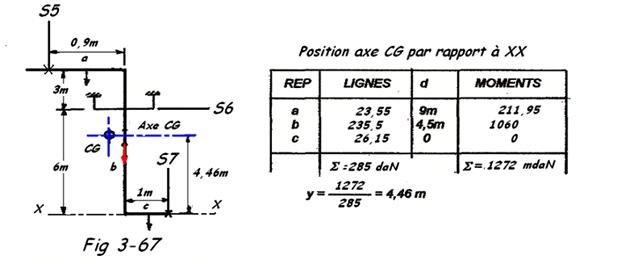
Calculons le CG entre S5 et S7 par rapport à l'axe XX.
Poids des tronçons
a = 0,9m x 26,15 da/m = 23,55 daN
b = 9m x 26,15 daN/m = 235,5 daN
c = 1m x 26,15 daN/m = 26,15 daN
NB : pour des calculs précis, il faudrait tenir compte des coudes, mais l'erreur commise est assez faible et n'influence donc pas la validité des calculs.
- On peut procéder de la même façon pour déterminer le CG par rapport à un axe passant ( par exemple) par S7. Dans notre cas, pour avoir une suspension stable, nous devons prendre le poids de celle-ci au-dessus du CG. Nous le situerons arbitrairement à 6 m de la base ( axe X-X ).
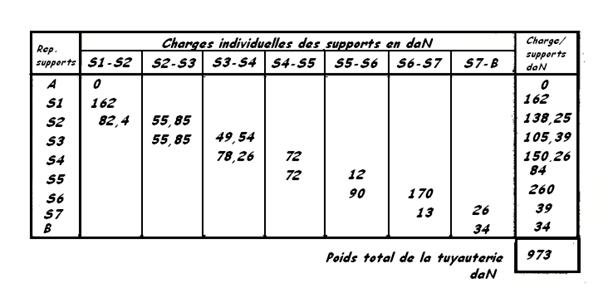
c) Calcul des charges
- Répartition des charges entre S1 et S2 Fig 3-68
Notons que la bride repère A ne peut être sollicitée.
∑ alg MS2 F = 0
- 82,4 x 2,2 - 7,7 x 1,9 + S1 x 1,5 - 49,7 x 0,95 = 0
Soit S1 = 162 daN
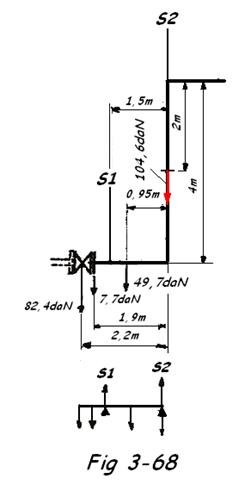
S2 = ∑ F - S1
∑ F = 82,4 + 7,7 + 49,7 + 104,6 = 244,4 daN
S2 = 244,4 - 162 = 82,4 daN
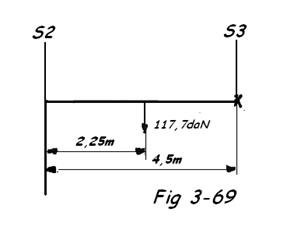
- Répartition des charges entre S2 et S3 Fig 3-69
- S3 x 4,5 + 111,7 x 2,25 = 0
Soit S3 = 55,85 daN
S2 = 111,7 - 55,85 = 55,85 daN
- Répartition des charges entre S3 et S4 Fig 3-70
Centre des moments en S3
Joindre S3 et S4 et porter perpendiculairement à ce segment de droite les forces gravitaires P1 et P2
( Poids du tube ).
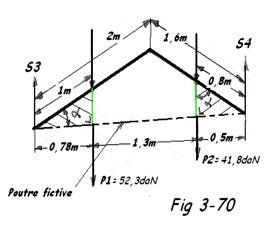
Tan α =
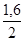
Cos α = 0,78 et sin α = 0,525
52,3 x 0,78 + 41,8 ( 0,78 + 1,3 ) - 54 x 2,58 = 0
S4 =
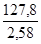
S3 = ∑ F - S4 = 127,8 - 49,54 = 78,26 daN
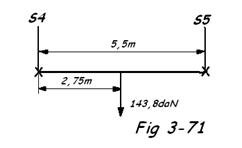
- Répartition des cherges entre S4 et S5 Fig 3-71
S4 = S5 =
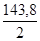
- Répartition des charges entre S5 et S6 Fig 3-72
Centre des moments en S5
- S6 x 0,9 + 78,5 x 0,9 + 23,5 x 0,45 = 0
Soit S6 =
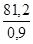
S5 = ∑ F - S6 = 102 - 90 = 12 daN
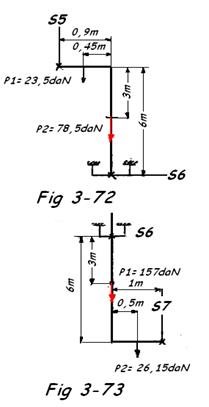
- Répartition des charges entre S6 et S7 Fig 3-73
Centre des moments en S6
- S7 x 1 +, x 0,5 + 157 x 0 = 0
Soit S7 ≈ 13 daN
S6 = ∑ F - S7
S6 = 157 + 26,15 - 13 ≈ 170 daN
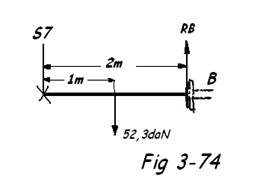
- Répartition des charges entre S7 et bride Rep B
( Fig 3-74 )
Centre des moments en S7
- RB x 2 + 7,7 x 2 + 52,3 x 1
RB ≈ 34 daN
S7 = ∑ F - RB = 26 daN
|
d) Calcul des déplacements
Dilatation thermique des tronçons pris individuellement et répartition des dilatations des tronçons à l'intérieur du système de tuyauterie
Δ1 =
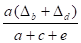
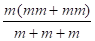
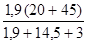
Δ2 = Δb - Δ1 = 20 - 6,37 = 13,63 mm
Δ4 =
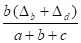
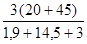
Δ3 = Δd - Δ4
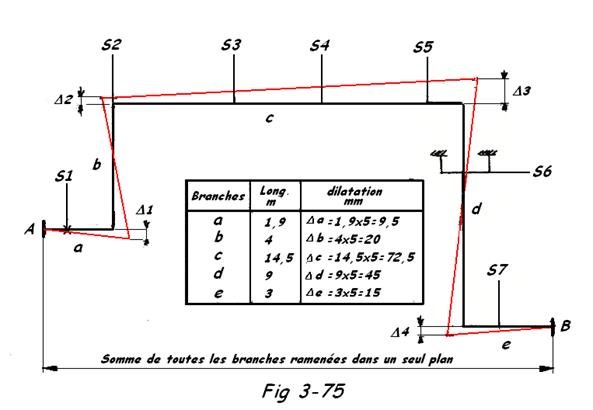
- Déplacements imposés aux supports pour la dilatation des branches à l'intérieur du système de tuyauteries considéré comme plan
- Déplacement du support S1 ( Fig 3-76 )
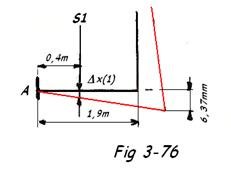
Δx(1) =
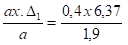
Le signe ( - ) car dirigé vers le bas
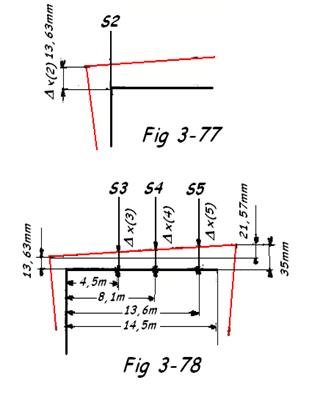
- Déplacement du support S2 ( Fig 3-77 )
Δx(2) = 13,63 mm ( signe ( + ) = vers le haut
- Déplacement du support S3 ( Fig 3-78 )
Δx(3) =
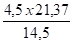
Signe ( + ) = vers le haut
- Déplacement du support S4 ( FIG 3-78 )
Dx(4) =
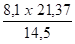
Signe ( + ) = vers le haut
- Déplacement du support S5 ( FIG 3-78 )
Dx(5) =
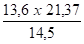
Signe ( + ) = vers le haut
- Déplacement du support S6 ( FIG 3-79 )
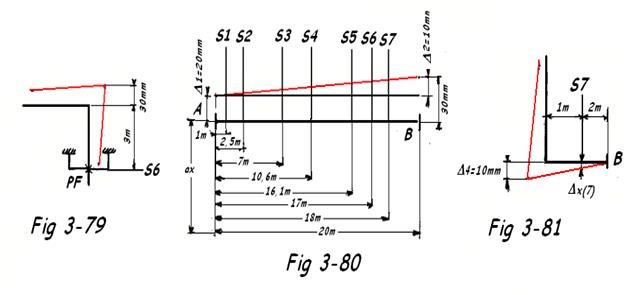
Dilatation verticale pour L = 3 m ; Δ = 3 x 5 mm/m = 15 mm
Δx(6) = 35 - 15 = 20mmm . Signe (+) = vers le haut
Notons que si cette longueur était plus importante ( ex : 10 m ), nous aurions eu Δ = 10 x 5 = 50 mm
et Δx(6) = 35 - 50 = - 15 mm. Signe ( - ) = vers le bas.
- Déplacement du support S7 ( Fig 3-81 )
Δx(7) = -
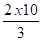
- Déplacement des supports dus aux déplacements du système de tuyauterie provoqués par des forces extérieures
Nous sommes dans le cas de la FIG 3-74 c soit Dx =
D1(S1) =
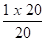
D1(S2) =
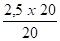
D1(S3) =
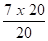
D1(S4) =
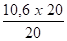
D1(S5) =
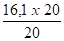
D1(S6) =
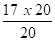
D1(S7) =
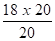
- Déplacements résultants des supports
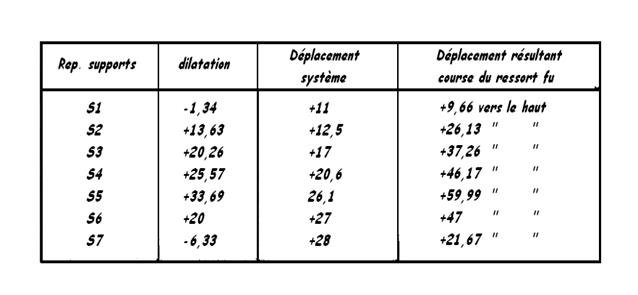
e) Choix du modèle et du type de supportage
Nous utiliserons dans ce problème des supports variables en partant des renseignements fournis par le catalogue SUPPORTAGE STANDARD 88 de ITT GRINNELL Gmbh.
Pour choisir le support adéquat, il faut d'abord déterminer son numéro en partant de la charge théorique à chaud telle que nous l'avons calculé ci-avant, et la repérer dans l'extrait du tableau FIG 3-94, puis on multiplie, pour ce numéro donné, la raideur du ressort avec la course verticale et on additionne ou soustrait cette valeur de la charge à chaud. Rappelons que pour un déplacement vers le haut, on additionne et pour un déplacement vers le bas, on soustrait. Cela donne la charge théorique à froid. Si cette charge à froid sort de la plage de course du tableau FIG 3-94, un autre support sera choisi. Pour ce faire, il existe les possibilités suivantes:
- Choix du support voisin, c'est-à -dire le numéro supérieur pour le déplacement vers le haut ou le numéro inférieur pour le déplacement vers le bas.
- Garder le même numéro de support, mais choisir un autre modèle avec une raideur de ressort supérieur.
Ainsi, dans notre problème, nous avions pour le support S1:
Course utile vers le haut = 9,66 mm soit 10 mm
Charge à chaud P1 = 162 daN soit 1620 N
Nous avons choisi un support type 6 pour une charge nominale de 1662 N proche de la valeur calculée
Cela nous donne pour une plage d'utilisation de 10 à 30 mm ( Fig 82 , type 6 de Grinnell => Fig 3-82 ), une raideur de ressort de 29,2 N/mm.
Charge à froid = Fc + Δ . K = 1620 N + 10 mm x 29,2 N/mm = 1912 N
Variation =
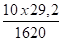
Position de montage
Pour 1589 N => déplacement utile = 10 mm
Pour 1662 N => déplacement utile = 12,5 mm
Soit pour 1662 - 1589 = 73 N, le déplacement est de 12,5 - 10 = 2,5 mm
1620 - 1589 = 31 N =>
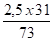
Soit la position de montage = 7,5 + 1,06 + 10 = 18,56 mm < 30
Il en sera de même pour les autres ressorts qui seront tous du type variable, mais attention à l'instabilité de la tuyauterie.
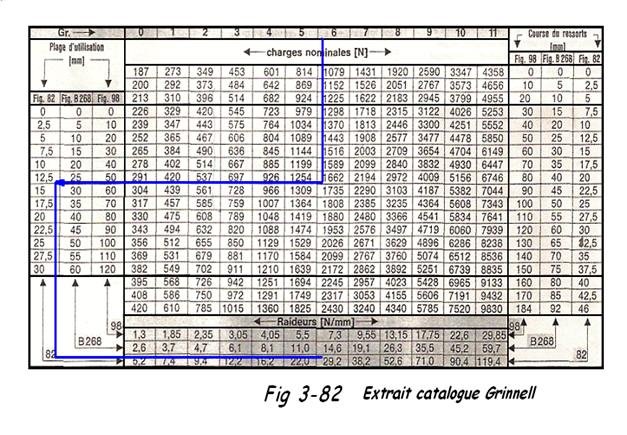
Pour le support S2 => Fig 98, type 4
Pour le support S3 => Fig 98, type 3
Pour le support S4 => Fig 98, type 4
Pour le support S5 => Fig 98, type 3
Pour ce support, la course utile est très importante ≈ 60 mm, mais la charge est faible. Un peut encore adopter un support variable.
Pour le support S6 => Fig 98, type 7
Pour le support S7 =>Fig B268,type 0
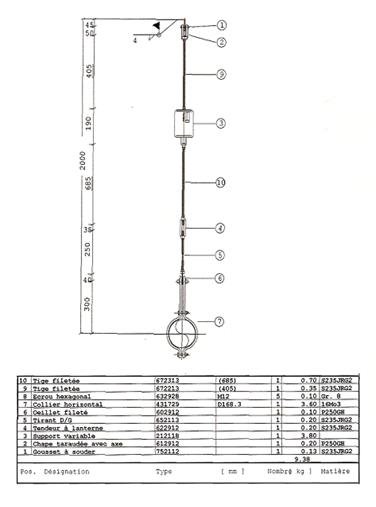
Les sociétés telles que LISEGA et PSS GMBH ( Grinnell ), donnent parfois, via leurs représentants, un logiciel de calculs des supports à ressort avec sortie graphique précisant les cotes de montage, ainsi qu'une nomenclature quantitative et
qualitative du matériel nécessaire au supportage ( ex. voir Fig 3-83 ).
Dernière édition: