8.6 CRITERE DE LIMITE ELASTIQUE
8.6.1 Conditions théoriques de résistance
Afin de réaliser des composants, on doit lors de la conception d'une pièce, s'imposer une limite supérieure aux contraintes sollicitant les matériaux.
- - Si le matériau est ductile et malléable, la référence sera la limite élastique Re
- - Si le matériau est fragile, la référence sera alors la résistance à la rupture Rr
- - Si les contraintes sont bi axiales voir même tri axiales, d'autres critères sont alors nécessaires tels que les critères de Rankine, de Tresca et de Von Mises pour les plus connus.
8.6.2 Critère de Rankine (Fig. 8-14 )
2. Remarque :
- Dans l'état plan de contraintes avec
- Pour un état de cisaillement pur
8.6.3 Critère de Tresca ( Fig. 8-15 )
1. Enoncé : La contrainte équivalente Ä·eq en tout point d'un matériau doit être inférieure ou égale à la contrainte limite d'élasticité à la traction Re ( ou à la compression si c'est le cas et que celle-ci est différente ).
En fonction des contraintes normales principales, ce critère peut s'écrire comme suit :
2. Remarques
- Ce critère donne de bons résultats dans le cas de sollicitations composées, si le matériau satisfait au mieux à Rge = 0,5 . Re ( ex. acier doux S235 ).
- pour les poutres soumises à des sollicitations normale et tangentielle :
8.6.4 Critère de Von Mises ( ou de l'énergie de déformation ) Fig. 8-16
Un matériau, lorsqu'il est déformé par une charge extérieure, tend à stocker de l'énergie interne dans son volume ( analogie avec les ressorts ).
Enoncé : On définit une contrainte équivalente
Le domaine élastique est défini par la relation :
Etat plan de contrainte (
Note :
Si on compare les deux critères précédents ( Fig. 8-16 ), on constate que c'est le critère de Tresca qui est le plus sévère .
- Pour les poutres soumises à des sollicitations normale et tangentielle :
Le critère de Von Mises est le plus souvent utilisé dans les calculs théoriques et dans les logiciels de calculs par éléments finis, en raison de la simplicité de son expression.
8.6.5 Critère de Mohr
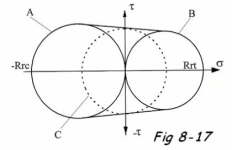
Pour beaucoup de matériaux, les résistances à la rupture en traction Rrt et en compression Rrc diffèrent. Le critère de Mohr basé sur des essais expérimentaux, prend en compte cette différence (Fig.8-17 ).
- Le cercle A traduit une sollicitation de compression simple.
- Le cercle B traduit une sollicitation de traction simple.
- Le cercle C traduit une sollicitation de cisaillement simple.
8.6.6 Critères pour matériaux fragiles (critère de Coulomb )
Schématiquement, lorsqu'un matériau fragile est soumis à un essai de traction, sa rupture se produit sans déformation plastique préalable.
Les contraintes maximales atteignent la limite de rupture Rr. Le critère de Coulomb ( ou de la contrainte normale maximale ) s'écrit :
8.6.7 Exercice résolu
Dans la zone la plus sollicitée d'une pièce chargée, on relève l'état de contrainte suivant :
On demande :
- De comparer les contraintes principales à la limite élastique
- D'appliquer le critère de Tresca.
- D'appliquer le critère de Von Mises.
1. Contraintes principales
Les contraintes principales sont inférieures à Re = 270 N/mm² en valeur absolue.
2. Critère de Tresca
3. Critère de Von Mises



Pièces jointes
Dernière édition: