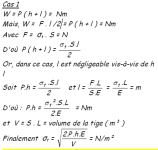CHAPITRE 3 : TRACTION OU EXTENSION
3.1 DEFINITION
Une poutre ou une barre est sollicitée à la traction lorsqu'elle est soumise, à ses deux extrémités, à l'action de deux forces ( N ) égales et opposées portées par la ligne moyenne et tendant à allonger cette poutre. ( Fig. 3-1).
Exemples : Les câbles soulevant un ascenseur.
La courroie qui transmet le mouvement d'une poulie à l'autre. Boulons fixant le fond d'un cylindre contenant un fluide sous pression.
3.2 EQUATION DE STABILITE ELASTIQUE
3.2.1 Notion de contrainte normale
Considérons une barre rectiligne ( Fig. 3-2a ) de section droite ( S ), soumise à un effort normal ( N ) dirigé suivant l'axe x x' et uniformément répartie sur toute cette section. Chaque unité de surface recevant de ce fait une force ni = N/S, N étant la résultante de ces forces, elle est appliquée au centre de gravité de la section. Sous l'effet de cette force, la barre se déforme et cette déformation se traduit, dans ce cas, par un allongement des fibres (
Le tronçon A ( Fig.3-2b ) sera en équilibre, si les forces intérieures ( ni ) par unité de surface, agissant sur la section droite ( S ) et normales à celle-ci, équilibrent la force extérieure N à condition de négliger le poids ( P = m . g ) de tronçon A, ce qui est généralement le cas en RDM ( le poids étant souvent très faible vis à vis des forces extérieures ).
A l'équilibre ; N - ( ni . S ) = 0
La force intérieure par unité de surface et normale par rapport à celle-ci est appelée " Contrainte normale de traction
N = effort de traction ( daN )
S = section de la poutre ( barre ) en mm²
Remarques : 1) La section prise en considération est la section nette, c'est à dire la plus faible section de la pièce constituant la section dangereuse ( ex. surfaces hachurées de la Fig. 3-3a,b ).
2) Lorsque le poids ( P ) de la barre ( force gravitaire ) n'est pas négligeable, l'équation d'équilibre devient :
3) lorsque les boulons ou les rivets sont placés en quinconce, la rupture peut se produire suivant la section ABCD ( 2 trous à déduire ) pour autant que cette section soit inférieure à la section EF ( Fig. 3-3c ).
Normalisation :a) Pour la NBN B51001
Relation dans laquelle N = effort ( non pondéré ) exprimé en daN et Sn = section nette exprimée en mm².
b) Pour l'Eurocode 3 ( acier )
Il faut vérifier que Nu
Nu = effort ultime en daN et Np = effort pondéré appliqué à la poutre en daN tel que
Exemples: Pour les charges permanentes on multiplie G par 1,35
Pour les charges d'exploitation Q par 1,5
4) Notes constructives : Lignes théoriques des barres ( lignes de trusquinage )
Dans les schémas des fermes,les barres sont représentées par un simple trait qui doit correspondre théoriquement à la fibre neutre (ligne moyenne) de leur section, c'est à dire passant par le centre de gravité. Afin de faciliter le traçage, on considère, en pratique, que cette ligne est donnée par l'axe de trusquinage. Pour les fers plats, la ligne de trusquinage se situe au milieu du plat, il en est de même pour l'âme des fers U. Pour les ailes des fers U et des cornières, la ligne de trusquinage se détermine en réalisant un petit calcul : ( Largeur de l'aile + épaisseur de cette aile ou âme ) divisé par deux. Porter cette distance à partir du dos de ces profilés.
Pour les poutrelles ( Fig. 3-5) on adopte la relation m =( b + e ) / 2.
Souvent, on se rapproche des bords de l'aile afin de dégager les boulons ou rivets de l'arrondi, mais il faut veiller à ce que n
3.2.2 Condition de résistance
Pour des raisons de sécurité vues au § 1.10, la contrainte normale doit rester inférieure à une valeur appelée contrainte admissible ( ou pratique ) à la traction : Rtadm.
Rtadm =
Rtadm =
se < sr sont des coefficients de sécurité variant de 1,1 à 10 selon les domaines d'applications et très souvent normalisés.
Exemples : En construction métallique se = 1,5 pour l'acier et pour des forces autres que celles du vent ( se = 1,7 pour l'alu ). sr = 5 pour le bois et 10 pour les câbles d'ascenseur.
Il y a toujours lieu de consulter les normes constructives, ou les cahiers des charges prescrits par le client par exemple.
La condition de résistance produit simplement le fait que la contrainte réelle ne peut dépasser le seuil précédent :
Remarque : Une autre méthode dite aux états limites est utilisée dans les Eurocodes ( par exemple ) et consiste à appliquer un coefficient de majoration aux charges ( coefficients de pondération
3.2.3 Influence des variations de section
Si le solide étudié présente de fortes variations de section ( Fig. 3-6), les relations précédentes ne s'appliquent plus directement. Au voisinage du changement de section, la répartition des contraintes n'est plus uniforme et
Remarques : 1) En cas de charge dynamique, la contrainte
2) On peut trouver dans des ouvrages spécialisés, tel que le " Guide du dessinateur " édité par le CETIM en France ou dans divers ouvrages de RDM, un ensemble de courbes permettant de déterminer kt . La fig 3-7 a-f donne quelques courbes usuelles.
3) Dans des cas complexes, on peut faire appel à un logiciel de calculs par éléments finis tel que RDM6 du Professeur Y. Debard de l'IUT Le mans ( Fr ) du département GMP.
Exemple : Supposons une plaque métallique en ALU Au4G ( Re0,2 = 240 N/mm² ), ayant les dimensions précisées à la Fig. 3-8 et comportant deux encoches. Cette plaque est soumise à une charge uniformément répartie à la traction de 60 N/mm. Déterminer la contrainte maximale à la traction en A et B.
Solution:
En raison des encoches largeur 20 mm et profondeur 20 mm, il y a concentration de contrainte A et B.
Calculons les valeurs r/d et h/d de la Fig. 3-7
Fig 3-7:
La Fig. 3-9 montre les résultats des contraintes obtenues après plusieurs simulations et avec une discrétisation de 783 noe uds et 352 éléments, au moyen du logiciel RDM6. On constate que les contraintes maximales sont bien situées en A et B ( zone rouge ) et que la contrainte calculée est de 46,74 MPa ( N/mm²), ce qui représente une erreur relative de ± 6% par rapport à celle déterminée manuellement.
Exercice résolu:
Une barre de contreventement ( L 60x60x6 ) en acier doux type S235 avec Re = 23,5 daN/mm² est fixée sur un gousset ( Fig. 3-10) avec des rivets à˜ 16 ( trous à˜ 17 ) et interrompu au droit du croisement comme montré à la Fig.3-10.
Calculer la largeur du gousset et vérifier la contrainte dans la cornière sollicitée par un effort de traction N = 6000 daN.
Cela conduit à un coefficient kt = 2,34. On aurait pu obtenir une valeur proche de 44 N/mm², soit en densifiant ou en modifiant le type de maillage au droit des zones rouges. Nous reparlerons des éléments finis en fin de cet ouvrage.
Solution:
Section nette de la cornière Sn = 6 ( 60 + 54 - 17 ) = 582 mm²
Au droit de l'assemblage, cette section est remplacée par le gousset ayant une épaisseur ( e + 1 mm ) = 7 mm. Sa largeur nette est égale à 582/7 = 83,14 mm soit 84 mm.
Si on compte un seul trou à déduire, on aura comme largeur du gousset : 84 + 17 = 101 mm minimum.
3.2.4 Equation de déformation
En période élastique, cette équation se déduit de la loi de Hooke ( rappel: § 2.2.1 ).
l0 = longueur initiale de la barre ( mm )
N = force de traction ( daN )
S = section de la barre ( mm² )
Exercices résolus:
1. Un tirant de longueur lo = 6 m est formé d'un rond en acier doux ( S235 ) et soumis à un effort de traction N = 5400 daN. Déterminer le diamètre du rond pour qu'il résiste en sécurité ( se = 1,5 ), ainsi que sa déformation si E = 21000 daN/mm². Le poids propre de la barre sera négligé.
Solution:
Rtadm = Re / se = 23,5 / 1,5 = 15,67 daN/mm²
Rtadm = N / S => S = N / Rtadm = 5400 / 15,67 = 344,68 mm²
On constate que cet allongement est faible vis à vis de la longueur de la barre. Il en est généralement ainsi dans la plupart des constructions et de ce fait les déformations élastiques sont souvent négligeables.
2. On place un moyeu en acier ayant un alésage de 100 mm sur un arbre de diamètre 100,1 mm. Déterminer la contrainte dans le moyeu et vérifier si
3.2.5 Travail de déformation
1. Charge statique
La charge est appliquée lentement et graduellement. Sous l'effort appliqué, la tige se déforme. Le point d'application de la force se déplace, celle-ci
effectue donc un travail, c'est le travail de déformation.
Ce travail est proportionnel à la surface découpée par le diagramme. Le travail de P1 est proportionnel à OAC
Le travail de P2 est " à OBD
Dans la zone élastique, le travail est proportionnel à la surface d'un triangle ( S = b.h / 2 )
Soit : WD = P . l / 2
Conclusions :
a) Dans la zone d'élasticité, le travail de déformation est restitué au moment de la suppression de la force.
b) Dans la zone de déformation permanente, le travail emmagasiné par la pièce n'est plus entièrement restitué.
Surface OABD => proportionnelle au travail de déformation totale
" EBD => " au travail élastique ou restitué
" OABE => " au travail perdu ou permanent
2. Charge dynamique
Cas 1 : Appliquée avec choc ( Fig.3-14) ;
Cas 2 : Appliquée brusquement par choc ( Fig. 3-15)
Supposons une charge P tombant sans frottement sur un plateau en bout de tige. Sous le choc, la tige s'allonge d'une longueur ( l ), d'où un travail fournit par le travail de déformation de la tige, c'est à dire la surface OAC de la Fig. 3-16.



Pièces jointes
Dernière édition: