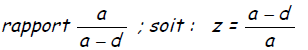3.8 ENVELLOPPES A PAROI MINCE SOUS PRESSION INTERNE
3.8.1 Généralités
Ces enveloppes peuvent être qualifiées de coques minces de révolution ou encore de coques axisymétriques à paroi mince sous pression interne.
a) Les deux formes principales que nous étudierons dans cet ouvrage, sont le cylindre et la sphère. L'EUROCODE EN 13445 précise que pour avoir une paroi mince calculable par les relations qui suivent, il faut que le rapport entre l'épaisseur de l'enveloppe ( ou virole ) ev et le diamètre extérieur de cette enveloppe ( de ) soit inférieur ou au plus égal à 0,16 soit ev / de
b) Pour le calcul de ces enveloppes, nous ne tiendrons compte, dans ce chapitre, que de l'influence de la pression et de la température.
c) Applications : les réservoirs, les ballons ( ballons de chaudières) Fig.3-37 contenant un gaz ou un liquide, les tuyauteries, . . sont des exemples.
d) Rappel de physique : La pression effective ( p ) est dans notre cas, la pression existant à l'intérieure de l'enveloppe, elle est mesurée au moyen d'un manomètre gradué en bar ( daN/cm² ).
La pression absolue ( pabs ) = pression effective ( p ) + la pression à l'extérieur de l'enveloppe ( pext ).
Généralement cette pression extérieure est la pression atmosphérique qui vaut en moyenne patm = 760 mm Hg = 10,33 mce =1,0134 bar. En pratique on adopte patm = 1 bar.
Notons que l'on utilise souvent l'unité barg pour désigner la pression effective.
3.8.2 Poussée résultante sur une demi-enveloppe
Toute enveloppe soumise à pression est essayée, avant mise en service, en présence d'un organisme agréé ( AIB-Vinçotte, Apragaz, . ) à la suite de laquelle cette enveloppe est acceptée ou refusée. Mais supposons que l'on poursuive cet essai jusqu'à la rupture de l'enveloppe, on constaterait que cette rupture se produirait par déchirure le long d'une
génératrice. Pour expliquer ce fait, prenons une enveloppe cylindrique à paroi mince soumise à une pression effective interne, de diamètre intérieur ( di ) et de longueur ( L ), fermée à ses deux extrémités ( Fig. 3-38 ). On peut isoler par la pensée une tranche de longueur infiniment petite (
symétriques M et M', centrés sur une surface
La force pressante en ces points sera F = p .
Calculons la résultante de ces forces en les projetant sur les axes ox et oy. On constate que chaque force pressante ( F ) admet deux composantes, l'une Fh parallèle à l'axe ox, l'autre Fv
parallèle à l'axe oy.
On constate :
a) Que la projection de la résultante sur l'axe ox est nulle, car aux deux points M et M' correspondent des forces Fh égales deux à deux et directement opposées (
b) Que la projection de la résultante sur l'axe oy sera
La résultante des forces pressantes sur la demi-enveloppes supérieure (1) aura pour valeur p . di .
La résultante des forces ( poussée ) sur l'ensemble d'une paroi demi-cylindrique de longueur L est égale à P = p . di . L
P est la poussée sur le rectangle CDD'C' ( Fig. 3-38) de surface di x L ( plan diamétral ). Ce raisonnement peut se faire à l'identique dans le cas des enveloppes demi-sphériques.
La résultante des forces pressantes sur la demi-sphère de diamètre di sera égal à
3.8.3 Contrainte transversale ( circonférentielle ) dans une enveloppe à paroi mince
Isolons la demi-enveloppe (1) comme indiqué à la Fig. 3-39. Celle-ci est soumise à la pression effective ( p ) et on négligera le poids mort. Les forces pressantes élémentaires ( p .
Si ev = épaisseur de l'enveloppe ( virole ) est faible, on peut admettre que la contrainte est constante dans toute l'épaisseur d'une section et N =
3.8.3 Contrainte longitudinale
Soit la Fig. 3-40, isolons au moyen d'une section droite, la partie (2) de l'enveloppe cylindrique close. La résultante N' des actions élémentaires exercées sur cette partie (2) par la partie (3), équilibre la poussée F' due à la pression effective exercée par le fluide sur l'intérieur du fond
Si l'on admet que la contrainte normale
On constate que la contrainte longitudinale est la moitié de la contrainte transversale, ce qui explique que la déchirure se produit suivant une génératrice.
La relation ci-dessus reste valable dans le cas des enveloppes sphériques, puisque la rupture se produit suivant un plan transversal. On peut constater que la forme sphérique permet de prendre une épaisseur deux fois plus faible que dans la forme cylindrique. Cependant, la réalisation d'un récipient sphérique est beaucoup plus onéreuse que celle du cylindre à fonds bombé ( Fig. 3-41).
3.8.4 Formules pratiques
Les formules établies dans le paragraphe précédent, sont valables lorsque les génératrices ont la même résistance ( continuité du métal ). Mais dans la pratique, les viroles sont réalisées au départ d'une tôle qui est roulée et ensuite rivée ou soudée. Il se crée un affaiblissement de la résistance au droit de la génératrice de raccordement ( joint ). Afin de tenir compte de cet affaiblissement, les normes comme l'Eurocode EN 134453, par exemple, préconisent l'utilisation des relations suivantes :
1. Enveloppes cylindriques
2. Sphères
z = coefficient de joint ( soudé ) =
- 1 ( contrôles destructif et non destructif )
- 0,85 ( contrôle non destructif par sondage )
- 0,7 ( contrôle visuel )
Rtadm = contrainte admissible ( N/mm² ) variant en fonction du matériau et de la température ( voir normes EN 10028 ).
c= surépaisseur de corrosion 0 à 3 mm pour l'acier laminé ( 0 adopté parfois pour l'inox ).
p = pression effective maximum de fonctionnement ( N/mm² )
ev = épaisseur de la virole arrondie à l'unité commerciale supérieure ( mm )
Tous ces équipements sous pression doivent satisfaire à la directive européenne 97/23/CE depuis 2002
Ces équipements sont essayés avant mise en service à une pression d'épreuve hydrostatique :
Dans laquelle : pmax = pression de fonctionnement maximale N/mm²
3.8.5 Fonds bombés
Pratiquement, on trouve deux grandes familles de fonds bombés.
1. Les fonds hémisphériques : ( Fig. 3-42)
Le calcul de l'épaisseur du fond ( ef ) est identique à ce que nous avons vu au paragraphe 3.8.5 pour le calcul des sphères. Autres formules intéressantes :
Volume intérieur du fond ( h1 = 0 ) : V = 2,094 . Ri³ = m³
Masse théorique du fond ( h1 = 0 ) : M = S . ef .8 avec S = 1,571 ( di + ef )² avec di et ef exprimés en dm et S = surface à la fibre moyenne .
LT = ligne de tangence
h1= bord cylindrique variable en fonction de l'épaisseur ef
2. Les fonds torisphériques : Ce sont des fonds bombés constitués d'une partie torique de raccordement et d'une enveloppe cylindrique.. Ces trois composants ayant des
tangentes communes aux points de raccordement. Pour le calcul, les prescriptions suivantes doivent être respectées :
On distingue : Les fonds bombés du type KLOEPPER appelés aussi fonds décimaux, pour lesquels Ri/de = 1 et rc/de = 0,1 ( Fig. 3-43)
Flèche intérieure ( mm ):
Surface du fond S = df² x 0,785 ( dm² ) avec df = 1,13(de - 0,65 . ef) + 1,5 . h1 + 0,2 ( dm )
Volume de la partie bombée ( h1 = 0 ) en litres
V = ( di + 0,25 )² x 0,5 h2 avec d1 et he en dm.
Les fonds bombés du type elliptique : Ce sont des fonds bombés dont la surface intérieure est à méridienne elliptique ( Fig. 3-44)
Flèche intérieure ( mm ):
Surface du fond ( dm² ) S = df² x 0,785 avec df = 1,2( de - 0,67. ef ) + 1,5 . h1 + 0,2 ( dm )
Volume de la partie bombée ( h1 = 0 ):
V = ( di . 1,06 )² x 0,466 . h2 ( di et h2 en dm )
Les fonds bombés du type KORBBOGEN : Ce sont des fonds dont la surface intérieure est à méridienne assimilée à un profil elliptique (Fig. 3-44), mais avec Ri=0,8 . de et rc = 0,154 . de ( rapport d'axes = +/2 )
Remarque : La hauteur de bord ( h1 ) est fonction de l'épaisseur du fond, par exemple :
h1 = 20 mm pour ef = 3 à 5 mm
h1 = 50 mm " ef = 13 à 14 mm
h1 = 90 mm " ef = 24 à 25 mm
Il y a toujours lieu de consulter le catalogue du constructeur.
3. Calcul des fonds torisphériques
L'épaisseur ef d'un fond torisphérique sera la plus grande des épaisseurs eS , ey , eb suivantes :
4. Raccordement virole fond :
Par soudure : Afin que celle-ci soit réalisée dans les meilleures conditions de résistance et pour satisfaire aux épreuves de réception ( radiographie, ultrasons, . ), si l'épaisseur maximum ( emax ) moins l'épaisseur l'épaisseur minimum ( emin ) est supérieur à emin/4, il faut réaliser un délardage, c'est à dire un chanfrein ayant une longueur au moins égale à ld = 4( emax - emin ).
3.8.7 Exercice résolu de calcul de 2 fonds bombés torispéhriques
Calculer l'épaisseur de l'enveloppe cylindrique et des deux fonds bombés torisphérique de type Kloepper d'un réservoir de 5 m³ de capacité, devant contenir un gaz ( N2 ) sous pression effective de 10 barg à la température de 20°C. Le diamètre extérieur sera de 1,5 m. Les coefficients de joint seront z = 0,85 pour la virole et z = 1 pour les fonds.
Matière : acier St37-2 ( 1.0308 ) avec E = 210000 N/mm² ; Re0,2t = 235 N/mm² et Rr20 = 340 N/mm²
Surépaisseur de corrosion c = 1.
Solution:
N2 = gaz non dangereux => Réservoir du groupe 2
Volume > 1 litre ; pmax = pression maximale admissible = 10 barg + 10% ( sécurité ) soit 11 barg ( 1,1 N/mm² )
ps . V = 11 x 5000 litres = 55000 soit d'après la Fig.3-47, la construction sera de la catégorie IV sans assurance qualité et devra subir une vérification CE. Epreuve hydraulique par organisme agréé à 1,43 x pmax. Il y a lieu d'établir une analyse
de risques ( voir Manuel des tuyauteries industrielles du même auteur ).
Calcul de l'enveloppe ( EN 13445 )
Calcul des fonds bombés type Kloepper ( décimaux )
Ri = de = 1500 mm ; rc = 0,1 x 1500 = 150 mm
Volume de l'enveloppe cylindrique = 5000 - 2 x 326 litres = 4348 litres



Pièces jointes
Dernière édition: