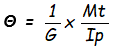Torsion, relations fondamentales

[rocdacier]

7.3 RELATIONS FONDAMENTALES

Dans ce qui va suivre, nous supposerons que les déformations restent dans le domaine élastique, et donc très petites.
Soient deux sections droites que nous appellerons S et S1 distantes d'une longueur très petite Δx.

L'essai de torsion a montré que la rupture a lieu suivant une section droite et qu'elle avait l'aspect d'une rupture par cisaillement. Donc, les forces qui agissent suivant cette section droite sont situées dans le plan de cette section. Le solide étant de section circulaire, homogène et isotrope, ces forces ne peuvent qu'être tangentes à  des circonférences concentriques (Fig. 7-5). Cette hypothèse peut être démontrée par la théorie de l'élasticité.

Rappelons que dans le cas général, la contrainte se décompose en une contrainte normale ( σ ) et une contrainte tangentielle ( Ï„ ). Dans le cas de la torsion simple ΔL ne varie pas, l'allongement ε = 0 et d'après la loi de Hooke σ = 0. Seules restent des contraintes tangentielles dont les vecteurs sont perpendiculaires au rayon ( Ï„g = G . γ ) et varient en fonction de celui-ci, Ï„ g = 0 en G et Ï„ g est maximum au rayon ( r ).

7.3.1 Equation de déformation élastique
Si nous voulons calculer les valeurs des contraintes tangentielles, il faut connaître la loi de répartition sur la section S. Pour cela, utilisons la relation établie lors de l'étude du cisaillement ( § 5.4 et 5.5.5 ) :

Pendant la déformation, le point M est venu en M'. Le déplacement MM' représente donc la dénivellation Δy correspondant à  la distance Δx ou MM' = ρ . Δx ( Fig. 7-6 ).

qui, par définition, mesure l'angle de torsion ( rad/mm ) est l'angle de torsion unitaire ( θ ). Par suite, ρ. θ = d'où : Ï„g = G . ρ . θ ( N/mm² = N/mm² x mm x rad/mm )

Note : Le radian est le rapport de deux longueurs ( π radians =

), c'est un nombre sans dimension. Rappelons que G est la contrainte transversale:

. La contrainte Ï„g en un point d'une section est proportionnelle à  la distance de ce point au centre de la section ( rappel § 6.4 ).

La force f appliquée à  un élément ΔS a pour valeur :

f = Ï„g . ΔS = ρ . G . θ . ΔS

Nous savons que Mt = d . F = Σ ρ . F => Mt = ρ . τg . ΔS

Soit : Mt = ρ². G . θ . ΔS , G et θ étant indépendants du choix du point M, nous pouvons écrire : Mt = G . θ . Σ ρ² . ΔS

Dans cette relation, Σ ρ² . ΔS représente le moment quadratique polaire Ip de la section S par rapport au point O, d'où : Mt = G . θ . Ip ( mmN = N/mm² x rad/mm x mm4 ).
De cette expression, nous pouvons tirer la valeur de l'angle unitaire de torsion correspondant à  des déformations élastiques.

7.3.2 Condition de rigidité
Pour les arbres de transmission tournant à  plus de 750 tr/min, on limite généralement la valeur de θmax à  0,5°/m, soit 0,5 . rad/mm. En dessous de cette vitesse de rotation on adopte généralement la valeur : θmax = 0,25 °/m.

​

7.3.3 Equation de résistance
De la relation Ï„g = G . ρ . θ remplaçons θ par sa valeur . Θ = , nous aurons :

Cette relation se différencie de la précédente, donnant la déformation, du fait que :
- Elle fait intervenir la position du point ( ρ = rayon )
- Elle ne fait pas intervenir la valeur de G ( c'est-à -dire le matériau ). Si on appelle ( V ) la distance la plus éloignée de la fibre neutre, donc la contrainte tangentielle de torsion sera maximale en ce point :

Remarques :

1. Dans cette étude, la section droite est circulaire de diamètre d. Le rapport Ip/V est souvent appelé " Module de torsion ". Dans le cas de notre cylindre, nous savons que

( § 6.4.3 ), or V = d/2 soit :

2. Nous savons que Ï„g est nulle au centre d'une section circulaire et maximum à  la périphérie, d'où l'idée d'utiliser des arbres creux afin de tirer un meilleur parti de la matière. Nous savons que pour une couronne circulaire ( Fig. 7-9 )

et le module de torsion prendra la forme

=> puisque V = d/2

On constate qu'à  égalité de contrainte et de moment de torsion, l'arbre creux exige une section moins grande donc une masse moindre au mètre Linéaire. Ainsi, pour d = 0,5 . D, on diminue la masse de l'arbre de 25%.