Cercle de Mohr

rocdacier · 31/8/21

8-3) Le cercle de Mohr

Toute l'information contenue dans les équations précédentes, peut être représentée sous forme graphique connue sous le nom de "Cercle de Mohr ". Celui-ci a été présenté pour la première fois en 1882, il représente la variation des contraintes normales et tangentielles dans tous les plans inclinés passant par un point ( M ). C'est une représentation commode des équations précédentes où les contraintes normales sont tracées le long de l'axe horizontal et les contraintes tangentielles le long de l'axe vertical.

Les contraintes

sont tracées à l'échelle et un cercle ayant son centre ( O ) sur l'axe horizontal ( x ) et passant par ces points est tracé ( Fig. 8-6 ). Cette figure montre le cercle de Mohr pour un élément soumis au cas général, pour un état de contraintes planes. Les coordonnées de la contrainte, sont la contrainte normale

et la contrainte tangentielle

sur une facette définie par

A partir de la Fig. 8-6, nous pouvons écrire que :

Théorème : La somme des contraintes normales sur deux facettes perpendiculaires, reste constante quand

varie.

3.Différents cas peuvent se présenter :

a) Lorsque deux contraintes principales sont de compression, dans ce cas le cercle de Mohr se trouvera à gauche de l'origine ( M ). Pour rappel, lorsque

= traction.

b) Dans le cas général, les contraintes en un point sont des tractions et des compressions. Le cercle de Mohr coupe l'axe des ordonnées.

c) Si les contraintes principales sont égales, le cercle de Mohr se réduit à son centre O. Toutes les facettes sont soumises à la même contrainte, uniquement normale ( état de contrainte hydrostatique plane ).

d) Construction inverse
Dans la pratique, on rencontre rarement le problème précédent, mais bien celui-ci. Si on connaît

et

sur deux facettes perpendiculaires quelconques, il faut rechercher la grandeur et la direction des contraintes principales.

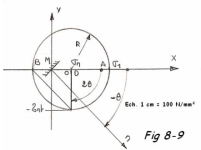
Pour construire le cercle de Mohr, on porte

. Pour obtenir les directions des facettes principales, nous supposerons que la première facette donnant

soit verticale. La facette

est par conséquent horizontale.

Menons une verticale par C et l'horizontale par C1, elles se coupent sur le cercle au point F ( Fig. 8-8 ). Les directions des facettes principales sont alors FA et FB. En effet, l'angle COA = 2

, l'angle CFA =

et l'angle BFA est droit en F.

Application
On connaît la valeur des contraintes normale et tangentielle sur les facettes orientées par x et y de la Fig. 8-4.

On demande de :
1. Déterminer la contrainte en C par ses composantes

2. Déterminer l'angle des directions principales, ainsi que les contraintes principales Ä·1 et Ä·2
3. Déterminer la contrainte en C pour une facette orientée par l'axe n, tel que

4. Retrouver le résultat précédent en utilisant le cercle de Mohr.