CHAPITRE 7 : TORSION
7.1 DEFINITION
7.1.1 Expérience
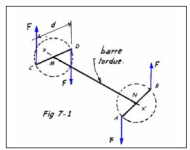
La Fig. 7-1 représente une barre rectiligne à laquelle, on applique, à ses extrémités, des couples égaux et de sens contraires dans des plans perpendiculaires à son axe géométrique x x'. Cette barre se déforme du fait que les bras de levier AB et CD tournent l'un par rapport à l'autre. Notons que l'un des couples peut être remplacé par un encastrement qui bloque tout mouvement.
7.1.2 Définition
Une section droite est soumise à la torsion, lorsqu'elle est sollicitée par un couple agissant dans le plan de la section, ou parallèlement à celui-ci. Ou encore, une poutre voir une partie de poutre est sollicitée à la torsion simple si, et seulement si, le torseur des actions de cohésion se limite à l'expression ci-contre. Le couple de forces donne un moment que nous appellerons "Moment de torsion ou couple de torsion
( Mt ) "soit :Mt = d . F (Unités : mN ou m.daN ou encore mm.N)
7.1.3 Hypothèses
Nous supposerons que :
- - Le poids du solide est négligeable
- - Le solide est une poutre homogène et isotrope
- - Toute section plane perpendiculaire à l'axe reste plane et perpendiculaire à l'axe après torsion, sans changer de forme.
- - La distance entre deux sections reste invariable, la longueur totale du solide ne changera donc pas.
- - L'angle dont les deux sections tournent l'une par rapport à l'autre est proportionnel à la distance de ces sections dont l'une est prise pour repère.
- - Un point sur la surface extérieure d'un cylindre décrit donc, dans ces conditions, une hélice (fig.7.2)
Un solide de forme cylindrique de révolution est parfaitement encastré à son extrémité gauche, suivant la section droite S1 de centre de surface G1 (Fig. 7-3).
On fait croître le couple Mt = d . F à partir de zéro et on mesure la déformation du cylindre. On constate que :
- - Toute section plane et normale à l'axe du cylindre, reste plane et normale à l'axe et invariable radialement.
- - La distance entre deux sections droites données reste sensiblement constante (allongement négligeable ).
- - Le déplacement d'une section droite S est uniquement une rotation d'angle ( α ) Fig. 7- 3 autour de son axe et cette rotation est proportionnelle à sa distance ( x ) à la section S1 : α = k . x
La génératrice M1 M2 se déforme suivant une hélice M1 M'2. Lorsque Mt croît, le dispositif enregistreur permet de mesurer α Mt = f( α ). La Fig. 7-4 représente le graphe d'un essai de torsion et on peut constater qu'il est semblable à celui d'un essai de traction pour un même acier.
Analyse de la courbe obtenue
Zone OA : C'est la zone des déformations élastiques. Si on réduit la valeur du couple Mt jusqu'à une valeur nulle, l'éprouvette va retrouver sa forme initiale.
Dans cette zone, l'angle α de torsion est proportionnel au couple appliqué.
Zone AB : C'est la zone des déformations permanentes. L'éprouvette ne retrouve plus sa forme initiale après déformation, elle subit donc une déformation permanente OO' , par exemple. L'essai se termine en D, par la rupture de l'éprouvette.
Angle unitaire de torsion:
Définition : On appelle angle unitaire de torsion ( θ )le rapport de l'angle de rotation d'une section droite quelconque à la distance qui le sépare de la section de référence (Fig. 7-3).
En torsion simple, l'angle unitaire de torsion est constant pour toutes les sections droites du cylindre.
Unités : α = radian ; x = mm = L et θ = rad/mm
Si L est exprimé en mètre, θ = rad/m ou en degré θ = °/m
( Rappel : 1° =



Pièces jointes
Dernière édition: