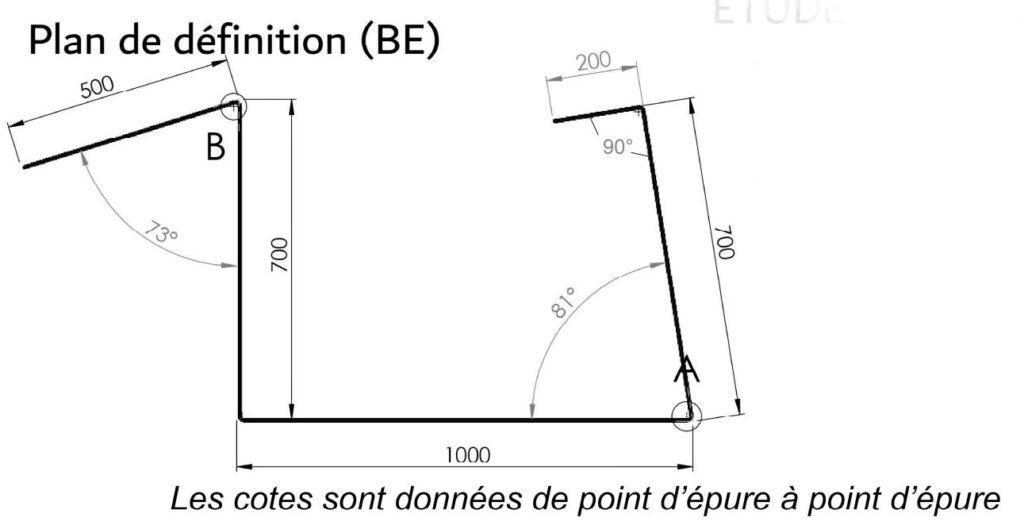
Sujet de l'étude
Mon collègue Fabrice a fait un exercice intéressant sur une pièce pliée avec des angles à 90° et des angles aigus. On a fait calculer la longueur développée avec plusieurs hypothèses. Des rayons intérieurs différents, des méthodes différentes et une position de la fibre neutre variable. Nous donnons une pièce en épaisseur 5mm en acier qui sera pliée avec un Vé de 40mm. Le Ri sera une fois de 6,5 mm et une fois de 7 mm. Comme les cotes sont données de point d’épure à point d’épure, on a un peu de calcul pour retrouver les cotes extérieures.
Extraits du plan de mon collègue:
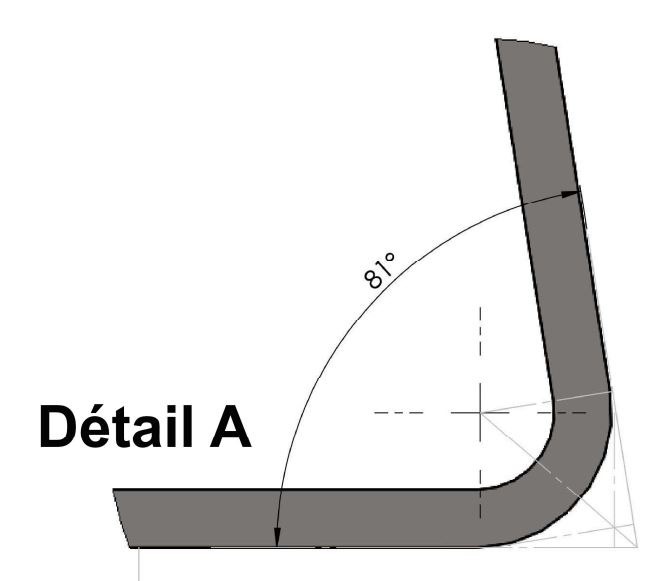
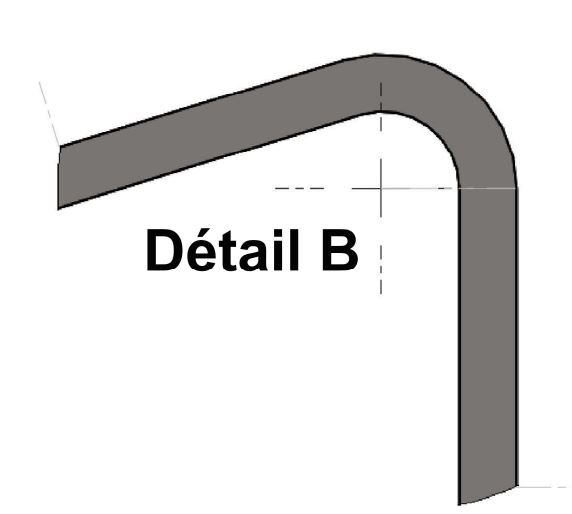
1ère méthode avec les abaques PROMECAM (DELTA L)
Avec cette méthode on va calculer en noir avec un Ri=6,5mm et en bleu avec un Ri=7mm
Tout d’abord pour utiliser les abaques des DELTA L ΔL (PROMECAM), il faut transformer les cotes données par les modeleurs SolidWorks et INVENTOR aux points d’épures en cotes extérieures:
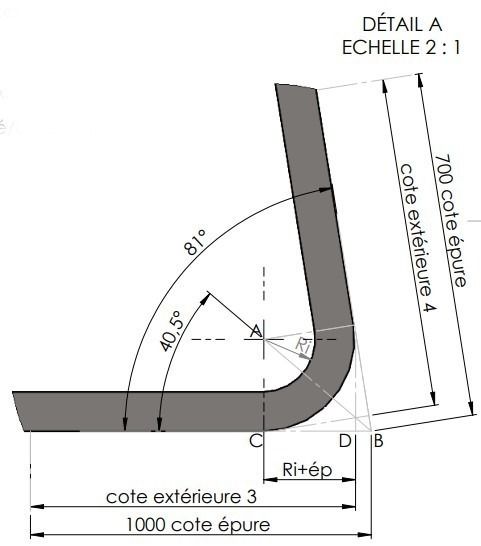
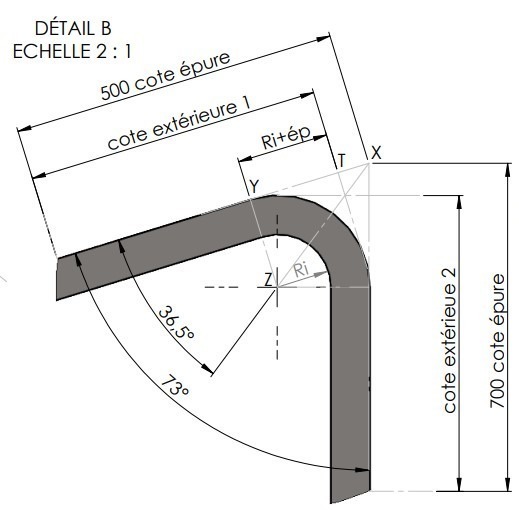
Si on commence par la cote extérieure 1, on doit faire 500-TX :
Cext1=500-TX ==> TX=XY-YT et YT = Ri+ep. YT=6.5+5 ==> YT=11,5mm (12 mm)
Pour XY, dans le triangle rectangle XYZ, on va utiliser la trigonométrie : tan36,5=YZ/XY ==> XY=YZ/tan36.5 avec YZ = Ri+ep donc YZ=11,5mm (12 mm) ==> XY=11,5/tan36,5 ==> XY=15,54 mm (16,21 mm) ==> TX=15,54-11,5 ==> TX=4,04 mm (4,21 mm)
Donc Cext1=500-4,04 ==> Cext1=495,96 mm (495,78 mm)
Pour la cote extérieure 2 (Cext2), on va utiliser la bissectrice de l’angle. Donc, le Cext2=700-TXèCext2=700-4,04 ==> Cext2 = 695,96 mm (695,78 mm)
On va utiliser la même méthode pour les cotes extérieurs 3 et 4 :
Cext3=1000-DB ==> DB=BC-CD et CD = Ri+ep. CD=6.5+5 ==> CD=11,5mm (12 mm)
Pour BC, dans le triangle rectangle ABC, on va utiliser la trigonométrie : tan40,5=AC/BC ==> BC=AC/tan40.5 avec AC = Ri+ep donc AC=11,5mm ==> BC=11,5/tan40,5 ==> BC=13,46 mm ==> DB=13,46-11,5 ==> DB=1,96 mm (2,05 mm)
Donc Cext3=1000-1,96 ==> Cext3=998,04 mm (997,95 mm)
Pour la cote extérieure 4 (Cext4), on va utiliser la bissectrice de l’angle. Donc, le Cext4=700-DB ==> Cext4=700-1,96 ==> Cext4 = 698,04 mm (697,95 mm)
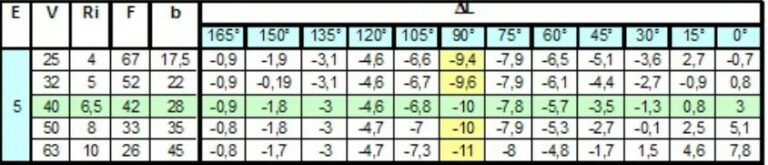
Pour connaitre le ΔL précis pour l’angle à 73°, on va faire une interpolation linéaire entre les valeurs 60° et 75° (ici nous sommes dans la théorie et dans la pratique nous aurions pu arrondir à la valeur de l’angle de 75° sans trop d’écart sur le résultat final).
Pour 60° et Vé de 40, ΔL=-5,7mm. Pour 75° et Vé de 40, ΔL=-7,8mm.
On a donc pour un écart de 15°, un écart sur le ΔL de 2,1mm. Etant donné que l’on cherche pour un écart de 2°, on va faire un produit en croix :
15°==> 2,1
2°==> x
x=2 x 2,1/15 ==> 0,28mm ==>ΔL (73°) = 7,8-0,28 ==> ΔL (73°) = 7,8-0,28 ==> ΔL (73°) = -7,52mm
Pour connaitre le ΔL précis pour l’angle à 81°, on va faire utiliser la même méthode : une interpolation linéaire entre les valeurs 75° et 90°.
Pour 75° et Vé de 40, ΔL=-7,8mm. Pour 90° et Vé de 40, ΔL=-10mm.
On a donc pour un écart de 15°, un écart sur le ΔL de 2,2mm. Etant donné que l’on cherche pour un écart de 6°, on va faire un produit en croix :
15° ==> 2,2
6° ==> x
x=6 x 2,2/15 ==> 0,88mm ==> ΔL (81°) = 7,8+0,88 ==> ΔL (81°) = 7,8+0,88 ==> ΔL (81°) = -8,68mm
Pour les deux angles à 90°, le ΔL est de -10mm.
On peut désormais calculer la longueur développée :
LD= Cext1-ΔL(73°)+Cext2-ΔL(90°)+Cext3-ΔL(81°)+Cext4-ΔL(90°)+200 :
Pour un Ri = 6,5mm :
LD= 495,96-7,52+695,78-10+997,95-8,68+697,95-10+200
LD= 3051,44 mm
Pour un Ri = 7mm :
LD= 495,78-7,52+695,96-10+998,04-8,68+698,04-10+200
LD= 3051,8 mm
2ème méthode avec calcul de la longueur de la fibre neutre
Si on utilise la méthode de calcul de la fibre neutre, on va chercher les longueurs droites et les longueurs courbes. Plusieurs combinaisons sont possibles. Si la fibre neutre est située à la moitié de l’épaisseur (1/2 ep), à un tiers de l’épaisseur (1/3ep) ou positionnée selon le facteur K (K-Factor). Ensuite, le rayon intérieur n’est pas une constante. Certains abaques le donnent à 6,5 mm et d’autres à 7 mm. On a vu précédemment que l’écart est très infime si l’on choisit un Ri de 6,5 ou un Ri de 7mm. Pour que l’étude soit la plus précise et exhaustive possible on va étudier les 5 combinaisons. Chaque portion sera découpée comme suit:
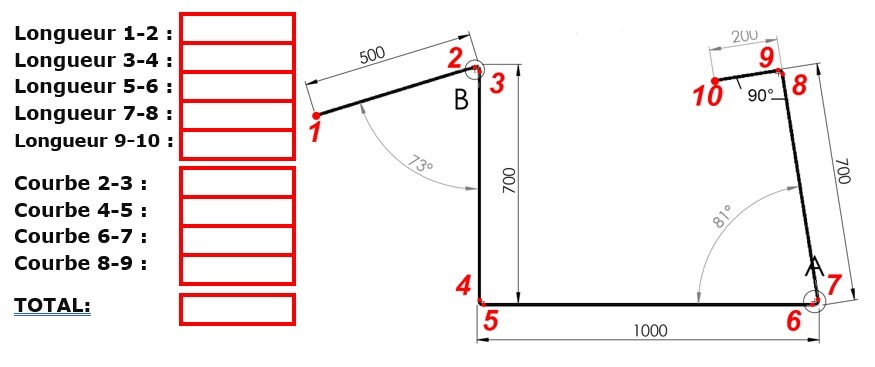
1ère combinaison: Ri=6,5mm et Fn positionnée à 1/2ep
La cote 1-2 correspond à 500-XT-(Ri+ep) ==> 1-2=500-4,04-(6.5+5) ==> 1-2=484,46 mm
La cote 3-4 correspond à 700-XT-(Ri+ep)-(Ri+ep) ==> 3-4=700-4,04-(6.5+5)-(6.5+5) ==> 3-4=672,96 mm
La cote 5-6 correspond à 1000-DB-(Ri+ep)-(Ri+ep) ==> 5-6=1000-1,96-(6.5+5) -(6.5+5) ==> 5-6=975,04 mm
La cote 7-8 correspond à 700-DB-(Ri+ep) ==> 7-8=700-1,96-(6.5+5) -(6.5+5) ==> 7-8=675,04 mm
La cote 9-10 correspond à 200-(Ri+ep) ==> 9-10=200-(6.5+5) ==> 9-10=188,5 mm
Pour les courbes on va utiliser la formule :
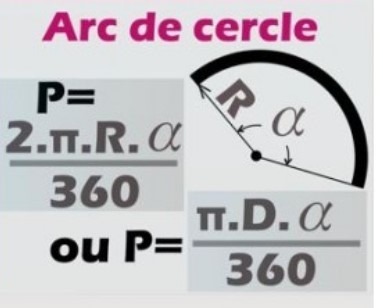
La courbe 2-3 est parcourue sur un angle de 107°(180°-73°) donc :
2-3 = 2 x PI x Rfn x 107/360
2-3 = 2 x PI x (6,5+2,5) x 107/360
2-3 = 16,81 mm
La courbe 4-5 est parcourue sur un angle de 90° donc :
4-5 = 2 x PI x Rfn /4
4-5 = 2 x PI x (6,5+2,5) / 4
4-5 = 14,14 mm
La courbe 8-9 est de même longueur donc 8-9 = 14,14 mm
La courbe 6-7 est parcourue sur un angle de 99°(180°-81°) donc :
6-7 = 2 x PI x Rfn x 99/360
6-7 = 2 x PI x (6,5+2,5) x 99/360
6-7 = 15,55 mm
On peut donc calculer la longueur développée en fibre neutre :
LD = 484,46 + 16,81 + 672,96 + 14,14 + 975,04 + 15 ,55 + 675,04 +14,14 +188,5
LD = 3056,64 mm
2ème combinaison: Ri=7mm et Fn positionnée à 1/2ep
Avec le Ri=7mm et Fn a 1/2ep:
La cote 1-2 correspond à 500-XT-(Ri+ep) ==> 1-2=500-4,21-(7+5) ==> 1-2=483,8 mm
La cote 3-4 correspond à 700-XT-(Ri+ep)-(Ri+ep) ==> 3-4=700-4,21-(7+5)-(7+5) ==> 3-4=671,8 mm
La cote 5-6 correspond à 1000-DB-(Ri+ep)-(Ri+ep) ==> 5-6=1000-2,05-(7+5) -(7+5) ==> 5-6=973,95 mm
La cote 7-8 correspond à 700-DB-(Ri+ep) ==> 7-8=700-2,05-(7+5) -(7+5) ==> 7-8=673,95 mm
La cote 9-10 correspond à 200-(Ri+ep) ==> 9-10=200-(7+5) ==> 9-10=188 mm
La courbe 2-3 est parcourue sur un angle de 107°(180°-73°) donc :
2-3 = 2 x PI x Rfn x 107/360
2-3 = 2 x PI x (7+2,5) x 107/360
2-3 = 17,74 mm
La courbe 4-5 est parcourue sur un angle de 90° donc :
4-5 = 2 x PI x Rfn /4
4-5 = 2 x PI x (7+2,5) / 4
4-5 = 14,92 mm
La courbe 8-9 est de même longueur donc 8-9 = 14,92 mm
La courbe 6-7 est parcourue sur un angle de 99°(180°-81°) donc :
6-7 = 2 x PI x Rfn x 99/360
6-7 = 2 x PI x (7+2,5) x 99/360
6-7 = 16,41 mm
On peut donc calculer la longueur développée en fibre neutre :
LD = 483,8 + 17,74 + 671,8 + 14,92 + 973,95 + 16 ,41 + 673,95 +14,92 +188
LD = 3055,49 mm
3ème combinaison: Ri=6,5mm et Fn positionnée à 1/3ep
Les longueurs droites ne changeront pas. Seules les cotes courbes sont à recalculer avec un Rfn différent :
La courbe 2-3 est parcourue sur un angle de 107°(180°-73°) donc :
2-3 = 2 x PI x Rfn x 107/360
2-3 = 2 x PI x (6,5+1,67) x 107/360 (Le Rfn (rayon en fibre neutre est = à 1/3 de 5mm ==> 1,67mm))
2-3 = 15,26 mm
La courbe 4-5 est parcourue sur un angle de 90° donc :
4-5 = 2 x PI x Rfn /4
4-5 = 2 x PI x (6,5+1,67) / 4
4-5 = 12,83 mm
La courbe 8-9 est de même longueur donc 8-9 = 12,83 mm
La courbe 6-7 est parcourue sur un angle de 99°(180°-81°) donc :
6-7 = 2 x PI x Rfn x 99/360
6-7 = 2 x PI x (6,5+1,67) x 99/360
6-7 = 14,12 mm
On peut donc calculer la longueur développée en fibre neutre à un 1/3 de l’épaisseur :
LD = 484,46 + 15,25 + 672,96 + 12,83 + 975,04 + 14,12+ 675,04 +12,83 +188,5
LD = 3051,03 mm
4ème combinaison: Ri=7mm et Fn positionnée à 1/3ep
Avec notre Ri=7mm.
La courbe 2-3 est parcourue sur un angle de 107°(180°-73°) donc :
2-3 = 2 x PI x Rfn x 107/360
2-3 = 2 x PI x (7+1,67) x 107/360 (Le Rfn (rayon en fibre neutre est = à 1/3 de 5mm ==> 1,67mm))
2-3 = 16,2 mm
La courbe 4-5 est parcourue sur un angle de 90° donc :
4-5 = 2 x PI x Rfn /4
4-5 = 2 x PI x (7+1,67) / 4
4-5 = 13,62 mm
La courbe 8-9 est de même longueur donc 8-9 = 12,83 mm
La courbe 6-7 est parcourue sur un angle de 99°(180°-81°) donc :
6-7 = 2 x PI x Rfn x 99/360
6-7 = 2 x PI x (7+1,67) x 99/360
6-7 = 14,98 mm
On peut donc calculer la longueur développée en fibre neutre à un 1/3 de l’épaisseur :
LD = 483,8 + 16,2 + 671,8 + 13,62 + 973,95 + 14,98 + 673,95 +13,62 +188
LD = 3049,92 mm
5ème combinaison: Ri=6,5mm et Fn positionnée selon le facteur K (K-Factor)
Les logiciels de type modeleur Inventor, Solidworks, etc, permettent d’intégrer la position de la fibre neutre. Cette position est le rapport distance entre la peau intérieure de la tôle et fibre neutre et épaisseur de la tôle. Pour nous ce serait distance/épaisseur.
Le facteur k (k-factor) pour notre configuration serait :
En admettant que le Ri 6,48mm soit ~ 6,5mm :
On a K-factor= position Fn/epaisseur ==> 0,349= position Fn/5 ==> position Fn=0,349×5 ==> position Fn=1,74mm
Notre Rfn cette fois-ci serait de 6,5+1,74 mm
La courbe 2-3 est parcourue sur un angle de 107°(180°-73°) donc :
2-3 = 2 x PI x Rfn x 107/360
2-3 = 2 x PI x (6,5+1,74) x 107/360
2-3 = 15,39 mm
La courbe 4-5 est parcourue sur un angle de 90° donc :
4-5 = 2 x PI x Rfn /4
4-5 = 2 x PI x (6,5+1,74) / 4
4-5 = 12,94 mm
La courbe 8-9 est de même longueur donc 8-9 = 12,94 mm
La courbe 6-7 est parcourue sur un angle de 99°(180°-81°) donc :
6-7 = 2 x PI x Rfn x 99/360
6-7 = 2 x PI x (6,5+1,74) x 99/360
6-7 = 14,24 mm
On peut donc calculer la longueur développée en fibre neutre positionnée selon le K-Factor:
LD = 484,46 + 15,39 + 672,96 + 12,94 + 975,04 + 14,24 + 675,04 +12,94 +188,5
LD = 3051,5 mm
3ème Méthode: Utiliser le calculateur de la CN CYBELEC
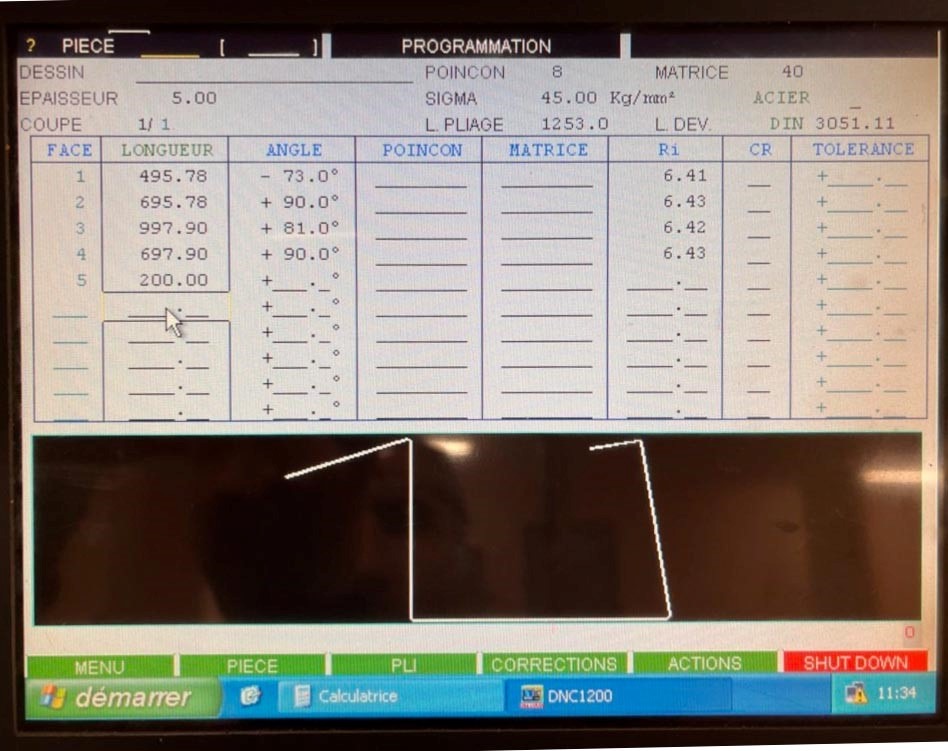
Que donnent les CN des machines presses-plieuses ?
Après avoir entré nos cotes extérieures, on obtient une longueur développée de 3051,1 mm. On constate que le Ri choisit par la machine évolue très peu en fonction de l’angle et qu’il est autour de 6,41 mm.
Conclusion
Avec nos différentes combinaisons de méthodes, de Ri et de position de la fibre neutre, on obtient diverses estimations des longueurs développées. On constate malgré tout qu’elles sont toutes très proches les unes des autres étant donné la grande dimension de la pièce.
Méthode des ΔL avec Ri=6,5 mm |
Méthode des ΔL avec Ri=7 mm |
Méthode de calcul de longueur de la fibre neutre par géométrie avec Ri=6,5 mm et Fn à 1/2 ep |
Méthode de calcul de longueur de la fibre neutre par géométrie avec Ri=7 mm et Fn à 1/2 ep |
Méthode de calcul de longueur de la fibre neutre par géométrie avec Ri=6,5 mm et Fn à 1/3 ep |
Méthode de calcul de longueur de la fibre neutre par géométrie avec Ri=7 mm et Fn à 1/3 ep |
Méthode de calcul de longueur de la fibre neutre par géométrie avec Ri=6,5mm et Fn proche de 1/3ep positionnée par K-Factor |
Méthode de calcul par la CN CYBELEC |
Méthode de calcul par les logiciels volumiques SOLIDWORKS/INVENTOR |
3051,5 mm |
3051,8 mm |
3056,6 mm |
3055,5 mm |
3051,0 mm |
3050,0 mm |
3051,5 mm |
3051,1 mm |
m |
Actuellement on constate que la LD est située entre 3050 mm et 3056,6 mm selon la méthode et les hypothèses choisies.
Les valeurs pour le Ri varient (pour les abaques PROMECAM on a Ri=6,5mm), pour de nombreux autres abaques on a Ri=7mm, voir 6,7mm. Si on prends le Ri donné par certains tableaux pour le K-Factor, j’ai Ri=6,48mm et pour la CN CYBELEC, on a un Ri=6,41mm.
On sait que sur les plis la position de la fibre neutre varie. On aura donc des valeurs différentes en fonction du cas où on place la fibre a 1/3ep, à 1/2ep ou a 0,349x ep (entre les 2) comme proposé par les tables du K-Factor.
L’idéal sera de procéder a un essai de pliage pour déterminer la LD exacte.
Produits Rocdacier
Quelques produits sont en vente sur le site : livres, posters, vêtements ignifugés, stickers…









