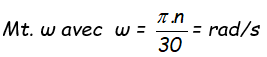7.4 CALCUL DES ARBRES DE TRANSMISSION
Il y a deux cas à considérer :
1. L'arbre est court (réducteurs, boîtes de vitesse, .. )
2. L'arbre est long (transmission de pont roulant, trépan, .. )
7.4.1 Arbres courts
On suppose, dans ce cas, que les charges ( engrenages, poulies, .. ) appliquées sur l'arbre ne peuvent le faire fléchir. L'arbre, de diamètre d, peut être calculé à la torsion et doit satisfaire à la relation
On peut établir la formule générale donnant le diamètre d'un arbre plein tordu en fonction de la puissance à transmettre (
Si nous exprimons la puissance en kW au départ, nous devons écrire :
Relation dans laquelle :
d = diamètre de l'arbre ( mm )
n = vitesse de rotation ( tr/min )
Rgadm = contrainte admissible à la torsion ( daN/mm² )
7.4.2 Arbres longs
L'arbre ne peut être sollicité que par un moment fléchissant de valeur faible. Pour ce faire, il faut placer les charges ( poulies, engrenages, .. ) le plus prés possible des paliers ( supports ). Toute variation brusque de la charge, peut entraîner une rotation importante des sections d'extrémité. De l'équation de déformation Mt = G . θ . Ip tirons la valeur de θ => soit : θ =
Formule dans laquelle :
n = vitesse de rotation ( tr/min )
d = diamètre de l'arbre plein ( mm )
7.4.3 Exercices résolus
1. Un arbre de transmission de navire tourne à la vitesse de 100 tr/min et transmet une puissance dé 10000 kW. Sachant que la résistance admissible à la torsion de l'acier utilisé est de 8 daN/mm² et que l'angle de torsion unitaire est fixé à 1 °/m, déterminer le diamètre minimum de cet arbre plein sachant que G = 8400 daN/mm².
Solution:
Condition de résistance:
Condition de déformation:
2. Un arbre tubulaire en acier Ni Cr ayant une contrainte admissible à la torsion de 40 daN/mm² et de longueur L = 1 m, est sollicité par un moment de torsion de 2100 mN. L'angle de torsion maximum toléré par les spécifications techniques du client est de 17°. Déterminer les diamètres extérieur D et intérieur d de cet arbre, sachant que G = 8000 daN/mm².
Solution:
Dimensions adoptées pour l'arbre tubulaire : D = 32 mm et d = 20 mm soit une épaisseur de 6 mm.
Remarques:
a) Nous pouvons facilement nous rendre compte que ce genre de problème ne possède pas toujours de solution satisfaisante. Pour obtenir une solution valable, il faut que
b) Les deux extrémités d'une barre de torsion doivent recevoir un bout d'arbre permettant l'application du moment de torsion, il s'agit souvent d'un bout d'arbre cannelé ou portant des stries, saillies, . sur une partie renforcée et raccordée au tube au moyen d'un congé de grand rayon. Il ne faut pas oublier que la sollicitation d'une barre est souvent une torsion alternée et qu'il faut vérifier que les contraintes maximales dues aux concentrations de contraintes, soient inférieures à Rgadm, mais plus précisément à la limite de fatigue.
3. La Fig. 7-10 représente le schéma d'une barre de torsion destinée à la suspension élastique d'un véhicule. Cette barre reçoit un effort de 1750 N agissant à l'extrémité d'un levier ayant une longueur de 200 mm. Déterminer : a) Le diamètre de la barre pleine, réalisée en acier 45 Si8 ayant une limite élastique Re = 650 N/mm², sachant que la sécurité sg = 2 et que le coefficient de concentration de contrainte aux raccords d'extrémité kt = 2,15.
b) La longueur maximale de la barre, afin que le levier ne puisse tourner plus de 6° 30' , lorsque le véhicule repose en charge sur ses roues. ( G = 81000 N/mm² )
Solution:
7.4.4 Utilisation d'un logiciel par éléments finis:
Nous utiliserons le logiciel RDM6, déjà référencié dans les chapitres précédents, pour vérifier la barre de torsion de l'exercice N° 3, ci-dessus. Nous avons préciser " Vérifier " car il faut nécessairement introduire la valeur du diamètre, la longueur de la barre, ainsi que les caractéristiques mécaniques du matériau (c'est le cas pour tous les logiciels de ce type ). Dans notre cas, le problème est géométriquement d'ordre spatial, nous utiliserons donc le module " Ossature " qu'il faut lancer en choisissant d'entrée une ossature spatiale + nouveau problème.
- - Définir les deux noeds extrémités de la barre Ax = 0 et Bx = 1020 mm, ainsi que la barre entre les deux noeds.
- - Dans le menu " Modéliser " choisir les commandes " Sections droites + paramètres + rond plein " => d = 25 mm
- - Choisir le matériau, ici 45 Si8, si celui-ci existe dans la bibliothèque, sinon il faut le créer dans le fichier " Matériau.dat ".
- - Encastrer le noed A à l'aide de la commande " Liaison " et cliquer sur l'icône " Encastrement " .
- - Pour placer ( Mt ) au point extrémité B, utiliser la commande " Cas de charge courant " et sélectionner " Couple nodal " => Mt = 350000 mmN.
- - Passer en mode " Calculer " puis sur " Résultats ".
- - Activer la commande " Isovaleurs " du menu " Résultats " puis " Cisaillement ". On obtient la carte des contraintes tangentielles de torsion ( Fig. 7-11 ). Soit ï´g = 114,1 N/mm²< à 120 ( 11,41 daN/mm² ) pour les fibres les plus éloignées de la fibre neutre.
La Fig. 7-11 nous rappelle que la répartition des contraintes de torsion dans une section circulaire, est d'intensité proportionnelle à la distance au centre.



Pièces jointes
Dernière édition: