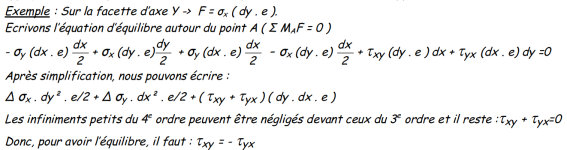Contraintes planes et élasticité plane

rocdacier · 30/8/21

8.1 INTRODUCTION

Il s'agit, dans ce chapitre, de réaliser une approche à la fois claire et très simplifiée des problèmes et des méthodes de la théorie de l'élasticité plane, afin de nous faire un idée de la complexité des phénomènes physiques qui régissent la distribution des contraintes et des déformations au sein d'un matériau sollicité par des forces extérieures.

8.2 CONTRAINTES PLANES

8.2.1 Hypothèses
Les principales sollicitations étudiées dans les chapitres précédents (traction, compression, cisaillement, torsion ) sont des exemples de contraintes planes. L'analyse de ces contraintes permet, non seulement de reproduire l'étude faites sur les sollicitations simples, mais permet également l'étude des cas complexes. Le principe consiste à découper la matière en petits cubes ( prismes ) élémentaires, afin de pouvoir réaliser une étude locale.

Rappels :
- On appelle contrainte normale (

), la projection de CM sur la normale extérieure ( n ).
- On appelle contrainte tangentielle (

), la projection de CM sur le plan de la facette

( Fig. 8-1 ).

8.2.2 Equilibre du prisme élémentaire

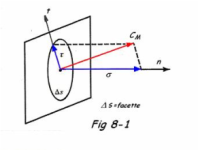
La Fig. 8-2 représente un prisme élémentaire de centre M. Nous nous occuperons ici, que des axes X et Y. Sur chaque face agissent deux contraintes définies ci-dessus, dont il faut compléter la désignation.

a) Convention d'écriture
- Chaque contrainte normale est définie par un indice représentant l'axe auquel elle est parallèle ( ex :

).
- Chaque contrainte tangentielle est définie par deux indices. Le premier représente l'axe auquel sa facette est normale, la deuxième représente l'axe auquel elle est parallèle ( ex :

).

b) Convention de signe
- Pour les contraintes normales, les contraintes de traction sont considérées positives et celles de compression, négatives.
- pour les contraintes tangentielles, elles seront positives si elles tendent à faire tourner le prisme dans le sens trigonométrique et négative dans le sens inverse. Ainsi pour la Fig. 8-2, les contraintes tangentielles sur les faces verticales sont positives et celles sur les faces horizontales sont négatives.

8.2.3 Réciprocité des contraintes tangentielles
Supposons que le prisme soit sollicité en traction dans les deux directions OX et OY. ( le sens des contraintes tangentielles n'est pas connu au préalable ). L'épaisseur du prisme " e = unité ". Les forces appliquées sont les produits des contraintes par les aires des facettes d'application.

En écrivant l'équilibre en rotation par rapport à Mx et My, on obtient un résultat analogue.

Théorème de Cauchy : Sur deux facettes perpendiculaires, les contraintes tangentielles normales à l'arête commune sont égales et se dirigent toutes deux vers cette arête ou s'en éloignent toutes deux ( Fig. 8-3 ).

Note : Les contraintes tangentielles doivent être disposées symétriquement par rapport à l'arête des facettes.

8.2.4 Contraintes planes dans une section inclinée

Etudions comment varie

) lorsque l'orientation de la facette change. Nous nous limiterons au cas particulier ou les contraintes restent dans un même plan, quelle que soit la facette considérée, ce qui constitue un état plan de contrainte très courant en RDM.

Voyons comment varient les contraintes sur les facettes normales au plan des contraintes, c'est-à -dire où les contraintes se projettent en vrai grandeur.

Pour ce faire, considérons un prisme dont la section est un triangle rectangle et dont l'épaisseur, perpendiculaire à la feuille, vaut l'unité. Soient la facette AB de section AB ; e = ds et M = centre de la facette.
dx = ds . sin

et dy = ds . cos

Equilibre du prisme ( Fig. 8-4)

- Equation de projection sur l'axe n (

)

La contrainte normale

dans tous les plans inclinés d'un angle

avec l'axe x est connue comme une fonction de

8.2.5 Contraintes principales
Nous savons que les contraintes planes varient en fonction de l'angle

, or pour le dimensionnement des pièces mécaniques, il est indispensable de trouver l'état de contrainte maximum.

Une contrainte est dite principale, lorsque sa direction est perpendiculaire au plan de la facette, c'est-à -dire lorsque

= 0. Cette condition permet de définir l'angle

. D'après les équations précédentes, nous pouvons écrire

Remarque : Dans notre cas :

En traction simple :

En cisaillement simple :

( on peut associer cet angle à l'angle que fait une fissure d'un linteau de porte près de l'appui, là ou l'effort tranchant est maximum ).

8.2.6 Contraintes tangentielles maximales