


1.3 LES HYPOTHESES DE LA RDM
1.3.1 Hypothèses sur les matériaux ( Fig 1.1 )
Les calculs réalisés dans le cadre des hypothèses communément admises en RDM sont fiables, si la matière possède les propriétés de continuité, d'homogénéité et d'isotropie.
ISOTROPIE : On admet que les matériaux ont, en un même point, les mêmes propriétés
mécaniques dans toutes les directions.

L'isotropie n'est pas vérifiée pour les matériaux tels que le bois, les matériaux composites, . etc
HOMOGENEITE : On admet que les matériaux ont les mêmes propriétés en tous les points.
CONTINUITE : On admet que les matériaux ne possèdent pas de fissures, pas de creux ... etc
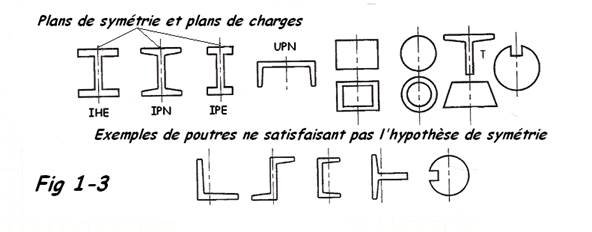
1.3.2 Hypothèses sur les formes ( Fig. 1.2 et 1.3 )
Les notions abordées dans ce cours, ne sont valables que pour des solides ayant une forme de " poutre " ; c'est-à -dire des solides pour lesquels ( Fig. 1.2 ) :
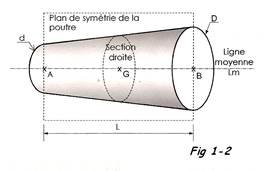
- On peut définir une ligne moyenne continue, reliant les barycentres des sections.
- Une des dimensions est très supérieure aux deux autres ( variable selon les matériaux ).
- Il n'y a pas de variation brusque de section ( trous, épaulements, . ).
- Il n'est admis qu'un seul plan de symétrie pour les charges et la géométrie.
1.3.3 Hypothèses sur les forces
Les forces ou actions mécaniques appliquées en un point, sont des vecteurs glissants. Il est impossible de les remplacer par un système d'actions mécaniques " vectoriellement " équivalent ( même résultante et même moment en un
point A ), car les effets physiques ( sollicitations ) sont différents. Le chargement se fait dans le plan de symétrie.
Il n'existe que deux types de chargement ( Fig. 1.5 )
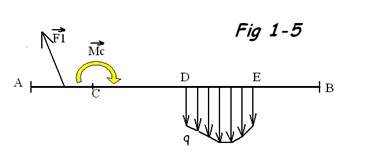
Soit une action mécanique :
- Localisée ( ou concentrée ) représentée par un glisseur ou .
- Répartie ( q ) représentée par sa densité linéique en N/m ou surfacique en N/m².
Exemple : Répartition uniforme de la neige sur un toit (charge surfacique) et glisseur équivalent au CG de la surface enneigée ( charge localisée ).
1.3.4 Hypothèse sur l'influence des déformations
Les déformations résultent et varient avec les actions mécaniques ( forces ou charges ) appliquées sur les objets. Elles sont mises en évidence par la variation des dimensions et peuvent être élastiques et réversibles ou plastiques et irréversibles.
Dans le domaine élastique, les déformations sont relativement faibles, elles ne modifient pas les actions mécaniques calculées par la statique ( hypothèse des solides indéformables ). L' élasticité caractérise l'aptitude que possède un matériau à reprendre sa forme et ses dimensions initiales après avoir été déformé. Par exemple, un ressort chargé normalement a un comportement élastique.
Remarques : Il n'existe pas de corps parfaitement élastiques, mais pratiquement tous les matériaux employés pour les pièces ou constructions n'accusent qu'une très légère déformation, aussi les considère-t-on comme parfaitement élastiques, pour autant que l'on ne dépasse pas un seuil ou la limite élastique. Dans le domaine plastique, le matériau ne reprend pas sa forme et ses dimensions initiales après avoir été déformé. Ainsi, par exemple, la pâte à modeler a un comportement plastique.
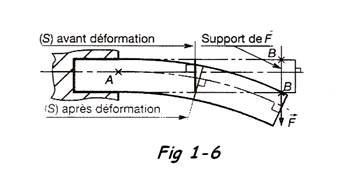
1.3.5 Hypothèse de Navier-Bernouilli
Les sections droites planes et perpendiculaires à la ligne moyenne restent planes et perpendiculaires à cette ligne après déformation. Il n'y a pas gauchissement des sections droites.
1.3.6 Hypothèse de Barré de Saint-Venant
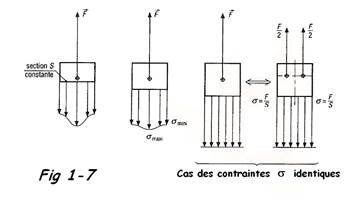
- Dans une section droite ( S ) éloignée de la zone ou les charges sont appliquées, la répartition des déformations et des contraintes ne dépend que des éléments de réductions des efforts de cohésion.
- Dans une section droite ( S ) proche de la zone où les charges sont appliquées, la répartition des déformations et des contraintes dépend de la répartition des charges appliquées.



Dernière édition:






