


5.4 SUPPORTAGE DES TUYAUTERIES DE FAIBLES dn
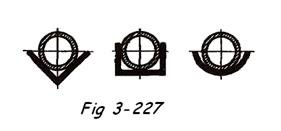
Pour les conduites horizontales, en particulier dans le cas de température " élevées " et pour de petits diamètres, un supportage continu peut être plus rationnel et plus économique qu'une fixation par colliers. La pose dans des cornières, profilés en U ou semi-ronds métalliques ou plastiques thermodurcissables a ainsi fait ses preuves. Notons que les extrémités de profilés seront ouvertes. En cas de danger de fuite prévoir une tuyauterie verticale de recueil de fuites. Il y a toujours lieux de fixer la tuyauterie dans le support en plaçant, de poste en poste, des colliers souples.
5.5 EXEMPLE DE CALCUL DE SUPPORTAGE
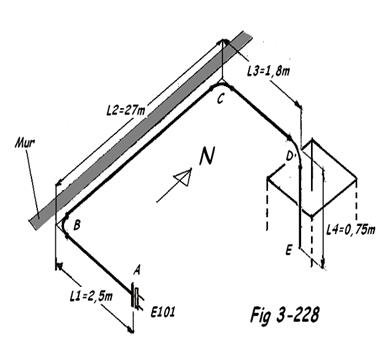
Données
Fluide véhiculé : H2SO4 69%
Masse volumique : 1580 kg/m³
Température de calcul tmax = 60°C
Température de montage = 20°C
Température mini de calcul = 10°C
Tube dn 100 ( de = 110 mm )
Qualité : PP-h ( homopolymère )
Accessoires à manchons soudés
Module de flexion ( 60°C ) : 750 N/mm²
Rt = 33 N/mm²
Module de fluage à tmax = 455 N/mm²
Module de fluage à tmin = 1125 N/mm²
La Fig 3-207 montre que nous devons adopter du PP-h classe Pn 100 soit
de = 110 mm ;
e = 10 mm ( di = 90 mm ).
α = 0,14 mm/m°C à 60 °C.
Déterminer le supportage, les efforts et les dilatations en considérant 2 hypothèses :
- En réalisant des lyres de dilatation
- En empêchant la dilatation dans le tronçon BC
Dt max ( sécurité ) = 60 - 20 = 40°C
DtBC = 27 x 0,14 x 40 = 151,2 mm
Solutions
1ère hypothèse : choix des lyres dans le tronçon BC
a) Vu l'importance de la longueur BC = 27 m, nous placerons 2 lyres verticales en prévoyant bien entendu une vidange au point bas entre les 2 lyres.
( 1,45² + 2 x 1,45 x 9 + 3 x 0,725 x 9 - 3 x 0,725² )
---- P x 1,45² x ------------------------------------------------------------- = L.D
E.I 3 ( 9 + 2 x 1,45 )
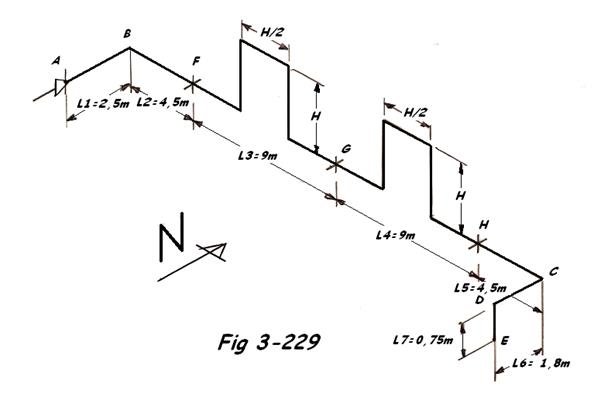
Soit ΔL entre FG et GH = 9 m x 0,14 x 40 = 50,4 mm. Ou encore ΔL' = ΔL/2 = 25,2 mm
Nous pouvons calculer H au moyen de la formule empirique H = k
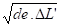
Soit H = 26
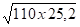
Adoptons H = 145 cm
Soit H/2 = 1450/2 = 725 mm
H/4 = +/- 350 mm
Poids du tube rempli d'acide
(3,01x9,81)+(
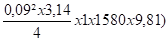
Q ≈ 130 N/m soit 1,3 N/cm
fmax = 6% du de, soit 6,6 mm, or le maximum est de 4 mm, nous adopterons cette valeur de
4 mm. Ef ( 60°C ) = 750 N/mm² => 75000 N/cm² et I =
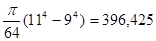
Calculons la longueur maximale entre 2 supports ( poutre sur 2 appuis ) avec C = 0,013
L =
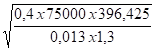
Lh ( pratique ) = 163 x 0,9 = 147 cm ( manchons soudés )
Lv = 1,3 Lh = 1,3 x 147 = 191 cm
Suivant la Fig 3-220 nous aurons L = 35 + 145 + 36,25 = 216,25 > 91 cm
Il faudra donc réduire les bras libres de +/- 26 cm
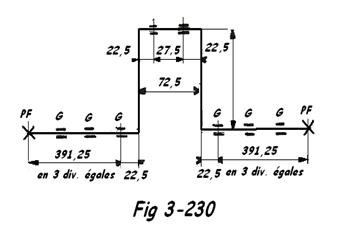
La Fig 3-230 nous donne 22,5 + 145 + 22,5 = 190 cm
Nous placerons deux supports sur la branche horizontale de la lyre, soit à 390 cm/3 = 130 cm < 147 cm
b) Etude du bras libre ABF ( Fig 3-231 )
ΔL1 = 2,5 x 0,14 x 40 = 14 mm
ΔL2 = 4,5 x 0,14 x 40 = 25,2 mm
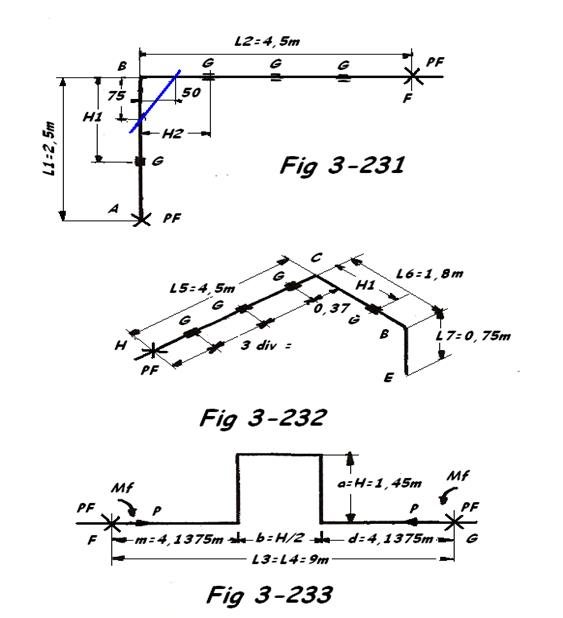
H1 = 28 x
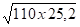
H2 = 28 x
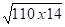
Mais ( H1 + H2 ) doit être inférieure à 163 x 0,9 =147 cm. Ce n'est pas le cas ici, il faudra placer des patins libres intermédiaires ( PL ) soit 50 + 75 = 125 < 147 cm.
c) Etude du bras libre HCDE ( Fig 3-.232 )
ΔL5 = 4,5 x 0,14 x 40 = 25,2 mm
H1 = 28 x
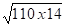
H1/4 =
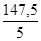
d) Calcul des efforts et moment aux points fixes ( méthode de Carlier ) Fig 3-233
Mf =
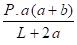
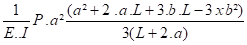
L . ΔL = 9 x 0,14 x 40 = 50,4 mm
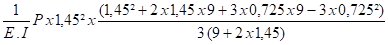
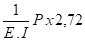
Mf =
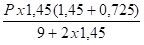
Or, Mf =
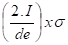
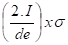
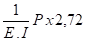
0,265 . P x 103 =
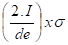
σ =
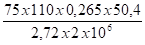
0,265 . P = 72,0773 cm³ x 0,02 daN/mm² soit : P = 5,5 daN ( valeur négligeable )
Mf = 5,5 x 0,265 = 1,46 mdaN
2 ème hypothèse : nous empêchons la dilatation entre les points B et c
Distance de supportage pour éviter le flambage
ΔL1 = 14 mm et ΔBC = 151,2 mm
Lf = 15,81
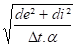
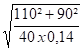
Nous proposons de diviser la longueur BC en 30 divisions égales de 900 mm ( entre axes des guides ) et la longueur AB en 3 divisions égales.
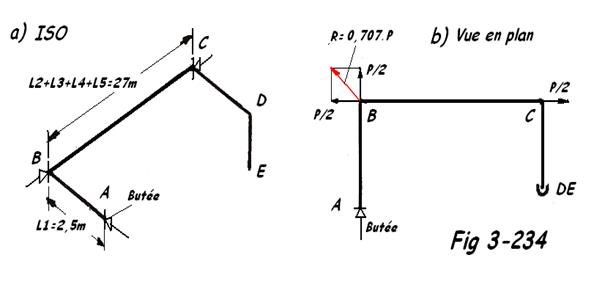
Calcul des efforts aux butées B et C
P =
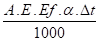
Ef ( 10°C ) = 1125 N/mm²
Ef ( 60°C ) = 455 N/mm²
Soit Ef =
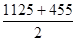
A =
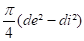
P =
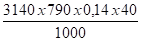
Sur les butées nous aurons P/2 = 13892 / 2 = 6946 N
Sur la butée B nous aurons P/2 ( AB ) et P/2 ( BC ) soit R = 0,707 X 13892 = 9821,7 N
Le point D est libre et ne donnera aucun effort sur C.
Nous constatons que les efforts sont trop importants. En outre, la dilatation du tronçon BC va imposer la pose de compensateurs de dilatation, de même pour le tronçon AB. De ce fait il faudra des supports guides de part et d'autre des compensateurs et provoquera un coût très important ainsi qu'un entretient plus coûteux.
Dernière édition:






